Crystallographic definitions for cube assemblies and ball-pyramid assemblies from poly-cubes and poly-balls, respectively

 

By Berchtold Frank Rordorf, Château d’Epanvilliers, Musee du Jeu Ancien, Feldpark 20, CH-6300 Zug

 

Abstract

 

Definitions in accordance with crystallographic nomenclature are proposed for all possible poly-cube assemblies up to 6 layer cubes and for all ball pyramids up to 8 layer tetrahedrons.  A new definition has thus also been given for the 3 layered 27-cube Soma–Cube as defined by Piet Hein, who used the term “non-regular” which was not in agreement with crystallographic nomenclature. 

 

Crystallographic restrictions have been introduced for both types of three-dimensional puzzles. Only poly-cube assemblies of the simple cubic structure are included.  Poly-ball assemblies with cubic densest ball packing and face centered cubic unit cell (fcc) only, leading to tetrahedral pyramids, are included.  It is shown that all poly-ball clusters to pentamers are both members of the cubic close packing (ccp) and the hexagonal close packing (hcp) structures.

 

A common nomenclature has been introduced for the poly-cube and the poly-ball clusters.  It is used up to tetramers for poly-balls and to pentamers for poly-cubes.    The number of possible spatial positions for these clusters in the simple cubic structure for the poly-cubes and in the face centered cubic for the poly-balls has been elucidated as a preparation for computer simulations for finding puzzle solutions.

 

Definitions in accordance with crystallographic nomenclature are presented for the 3-, 4- and 5-layer cube assemblies of the poly-cubes and for the 4-, 5-, 6-, 7- and 8-layer poly-ball pyramid assemblies.  Hand found solutions are presented for the 4- and 5-layer poly-cube assemblies and for the 5-, 6-, 7- and 8-layer poly-ball tetrahedron assemblies. The poly-cube clusters have been colored in a checkered fashion and in order to increase the challenge for finding solutions.

 

Introduction

 

A large community of puzzlers and mathematical recreation interested persons has studied the practical aspects of polycubes and polyominoes and an overview is given on the polypages of the internet site recmath.com [1, 2].  Most of this material has only been published on internet sites with a few exceptions such as the book in German by Ekkehard Künzell on games played with pentacubes [3].  The most systematic studies have been published by Thorston Sillke of the Mathematikum at the Bielefeld University in “Tiling and Packing results” [4].

 

On the other hand poly-cubes problems are widely treated in computing and combinatorics and are a popular problem in discrete geometry and an important tool in statistical physics for instance in computations related to percolation processes and branched polymers [5].  These publications are, however, in general out of scope for the puzzle and gaming community.  Again for polyball puzzles, information is only available on internet, and one of the most comprehensive publications is the document “Some Notes on Ball-Pyramid

and Related Puzzles” by Leonard Gordon [6].

 

The nomenclature of polyominoes for flat and polycubes for three-dimensional orthogonal cube clusters of the puzzle community has been dropped [1, 2, 3] and been replaced by a harmonized nomenclature for both poly-cube and poly-ball assemblies by adopting the standard nomenclature used in chemistry for polymers.  There are many excellent introductions for readers who are not familiar with crystallographic nomenclature and symmetry [7, 8] and a classic student introduction in crystallography for students [9].  As this paper should be accessible for the gaming community some basic concepts are presented here as an introduction.

 

Symmetry according to G. Burns [7] is a visual demonstration that an object is invariant to a given transformation. The symmetry transformations of the identity and of translation are trivial and will not be considered here.  Point symmetry operations are all of the transformations which are defined with respect to at least one point of the object which does not move during the operation.  These points are often, but need not be, identical with the points which define the lattices and the point groups.  A lattice is defined as an array of points in space with each point having identical surroundings.  The simplest way to generate such a lattice is by invoking translational invariance. Mathematically this process is described by applying translational symmetry by a primitive translation vector, which in turn is the sum of three spatial unit vectors for any three dimensional lattice.

 

Lattices are a mathematical concept and their introduction is essential in order to abstract from the complications of real life situations, such as encountered with molecules or crystals, and make these complex bodies amenable to symmetry considerations.  As an example let us consider a wooden cube: it has 8 corners, which define 8 visible points.  More important for the present consideration is the point formed by the intersection of the 4 space diagonals. In case of a homogenous cube this point defines its center of mass and can be used to describe the position of the cube in the lattice.  Likewise the position of a wooden ball in a crystal lattice can be described by using its radial center point. For symmetry considerations the constituting cubes or balls can thus be replaced by their center of mass points.

 

Describing the constituents of poly-cube or poly-ball puzzles by resorting to such lattice descriptions has some immediate consequences:  a single cube for instance, no longer has any symmetry at all.  Likewise, all flat poly-cube or poly-ball clusters no longer have the mirror symmetry with respect to the plane as defined by the center of mass points.

 

The three unit vectors which sum up to the primitive translation vector, also define a space, called the primitive unit cell of the lattice.  Primitive unit cells always contain only one single lattice point, in general the result of the sum of the contribution fractions of lattice points (for instance 8x 1/8^th of a lattice point for a simple cubic lattice). Often the unit cell defining a crystallographic lattice is, however, not a primitive unit cell, as for example for the face centered cubic structure of the cubic system.

 

Poly-cube puzzles

 

            All of the poly-cube assemblies discussed here and all of the resulting three dimensional puzzles built up from these clusters have a lattice unit cell which has the same dimension as the unit-cube of the puzzle.  This is a consequence of the crystallographic restriction to orthogonal assemblies only:  all neighboring cubes in all possible assemblies always share four corner points each. All assemblies are of the simple cubic structure, having one cube sitting on each corner of the cubic unit cell with a crystal lattice of the point group Pm3m (O¹_h) [7, p.193]. In the space group nomenclature of the 32 crystallographic point groups, Pm3m is the international symbol and O¹_h the Schoenflies-Symbol of the simple cubic structure.   

 

            The primitive unit cell is identical with the lattice unit cell in the simple cubic structure.  They in turn are identical with the space defined by the corner points of the translated unit cube, translated so that the center of mass point comes to sit on the lattice point.  Crystal systems are defined by symmetry elements and their effects on the unit cell dimension.  The most important symmetry element of the cubic symmetry group is the three fold axis and indeed there are four three fold axis present at angles of 109º 28’. This is a consequence of a symmetry law which states that only a single or a set of four 3-fold symmetry axes can exist.  

 

No	Object name	Letter & (Künzell) notation	Position count	Mirror planes	C2	C3	C4	Point group
1	PC_1F	1_I	1	4m+3m				4mm(C4v), Pm3m (O1h)
2	PC_2F	2_I	3	2m+m	2xC2			mm2(C2v), mmm(D2h)
3	PC_3F_180	3_I	3	2m+m	2xC2			mm2(C2v), mmm(D2h)
4	PC_3F_90	3_V	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
5	PC_4F_180_180	4_I	3	2m+m	2xC2			mm2(C2v), mmm(D2h)
6	PC_4F_180_90	4_L	24	m				1(C1), m(C1h)
7	PC_4F_90_270	4_N	12	m	1xC2			2(C2), 2/m(C2h)
8	PC_4F_90_90	4_O	3	4m+3m	4xC2		1xC4	4mm(C4v), 4/mmm(D4h)
9	PC_4F_180y90	4_T	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
10	PC_4T_90y0	4_A	8	3m+m		1xC3		3m(C3v), ‾6m2(D3h)
11	PC_4R_90_0	4_S1	24	m	1xC2			2(C2), 2/m(C2h)
12	PC_4R_270_0	4_L1	24	m	1xC2			2(C2), 2/m(C2h)
13	PC_5F_180_180_180	I (10)	3	2m+m	2xC2			mm2(C2v), mmm(D2h)
14	PC_5F_180_180_90	L (11)	24	m				1(C1), m(C1h)
15	PC_5F_180_90_180	V (13)	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
16	PC_5F_180_90_270	N (40)	24	m				1(C1), m(C1h)
17	PC_5F_90_180_90	U (90)	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
18	PC_5F_90_180_270	Z (20)	12	m	1xC2			2(C2), 2/m(C2h)
19	PC_5F_90_270_90	W (30)	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
20	PC_5F_180_90_90	P (60)	24	m				1(C1), m(C1h)
21	PC_5F_180_180y90	Y (12)	24	m				1(C1), m(C1h)
22	PC_5F_90_180y270	F (70)	24	m				1(C1), m(C1h)
23	PC_5F_180_90y270	T (80)	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
24	PC_5F_90y180y270	X (50)	3	4m+m	4xC2		1xC4	4mm(C4v), 4/mmm(D4h)
25	PC_5T_90_90_0	Q (61)	24	1m				m(C1h)
26	PC_5T_90_0_90	A (37)	24	1m				m(C1h)
27	PC_5T_180_90y0	L3 (81)	24	1m				m(C1h)
28	PC_5T_180y90_0	T2 (82)	12	1m				m(C1h)
29	PC_5T_180y90y0	T1 (51)	12	1m	1xC2			mm2(C2v)
30	PC_5R_180_90_0	L4 (41)	24					1(C1)
31	PC_5R_180_270_0	J4 (42)	24					1(C1)
32	PC_5R_90_270_0	N1 (31)	24					1(C1)
33	PC_5R_270_90_0	S1 (32)	24					1(C1)
34	PC_5R_90_180y0	J2 (72)	24					1(C1)
35	PC_5R_270_180y0	L2 (71)	24					1(C1)
36	PC_5R_90_270y0	N2 (33)	24					1(C1)
37	PC_5R_270_90y0	S2 (34)	24					1(C1)
38	PC_5R_90_180_0	J1 (22)	12		1xC2			mm2(C2v)
39	PC_5R_270_180_0	L1 (21)	12		1xC2			mm2(C2v)
40	PC_5R_90_0_270	V2 (35)	12		1xC2			mm2(C2v)
41	PC_5R_270_0_90	V1 (36)	12		1xC2			mm2(C2v)

 

Table 1.  All poly-cubes up to pentamers are listed.  For reference, the table also lists the nomenclatures for the poly-cubes by letters [4] and in brackets by Künzell [3]. Underlined bold angles point to the second layer. C2, C3, C4 indicate the presence of  2-, 3-, and 4-fold symmetry axis.  The point groups of the clusters are given both with (italic) and without the mirror plane (m) parallel to the surface of the flat pieces.

 

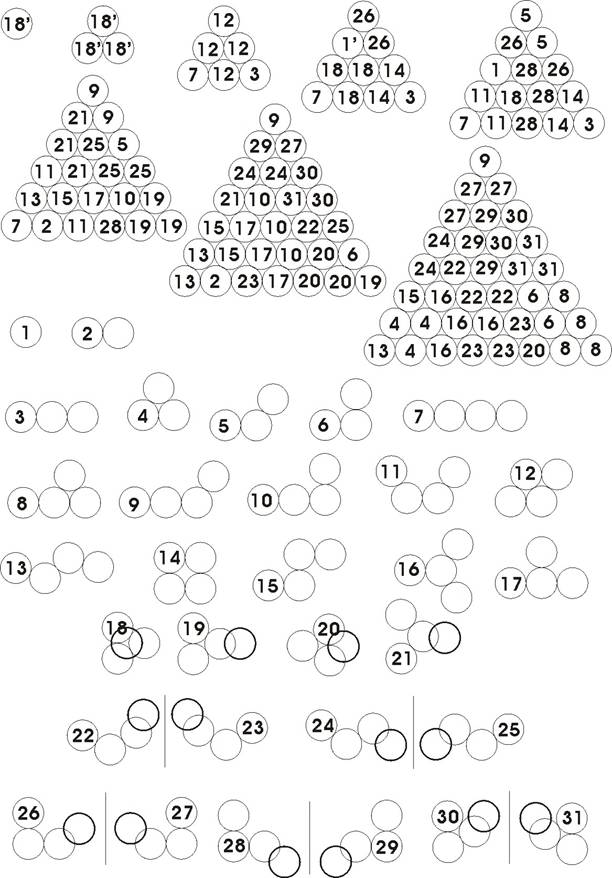
In order to define the poly-cube clusters the following nomenclature is introduced (see Table 1):  PC stands for Poly Cube, F for flat, T for three dimensional with a mirror plane, R for racemic (chiral); angles are 180 for straight and 90 / 270 for right angles, y indicates a branching, and _0 a change to the second layer for the next cube. In this case a more correct _90 , as used in case of the poly-balls, has been replaced by _0 for clarity.  The maximum number of assembled cubes lye on the surface and one starts out from the longest straight piece. Angles are given starting with the 3rd piece. Each cube can be treated as a point for defining the symmetry. All flat pieces would otherwise have an additional mirror plane (m) parallel to the surface of the flat pieces. The column labeled position counts indicates the number of possible spatial positions of each cluster in the cubic lattice (of course without translations). This information is useful for designing computer simulations for determining the maximum number of possible solutions to the puzzles.  Figure 1 shows the different poly-cubes as listed in Table 1. 

 

Table 2 presents a summary of the number of possible polymer of each type, flat, three-dimensional with at least one out of plane mirror plane, or in form of raceme pairs.  The number of constituting cubes is also indicated and these numbers were used for finding unique definitions for the different poly-cube assemblies forming cubes again.

 

Table 2. Summary of poly-cube assemblies:

 

	Flat	Number of cubes	Three-dim. non chiral	Number of cubes	Racemes	Number of cubes	Total cubes
Monomer	1	1					1
Dimer	1	2					2
Trimer	2	6					6
Tetramer	5	20	1	4	2	8	32
Pentamer	12	60	5	25	6x2=12	60	145
							186

 

Unique definitions for the macroscopic poly-cube assemblies up to the 6 layer cube:

 

- The 2 layer 8-unit cube can be assembled from all pieces up to trimers, while the linear trimer is replaced by a dimer.

 

- The 3 layer 27-unit Soma-Cube can be assembled from the non-regular poly-cube pieces up to tetramers (Piet Hein Definition).

 

- The 3 layer 27-unit cube can also be assembled from all flat pieces up to tetramers, while the linear tertamer is replaced by a dimer.  Therefore the clusters 1, 2x2, 3, 4, 6, 7, 8, 9 of Table 1 and Figure 1 are used.

 

- The 4 layer 64-unit cube can be assembled from the flat pentamers (11x4), while the linear pentamer is replaced by the linear dimer, trimer and tetramer pieces (2+3+4 = 9).

                

- The 5 layer 125-unit cube can be assembled from all pentamers pieces except the four raceme pieces with a symmetry axis.

                

- The 6 layer 216-unit cube can be assembled from all clusters to pentamers, plus the linear and the three dimensional non-raceme pentamer pieces.

 

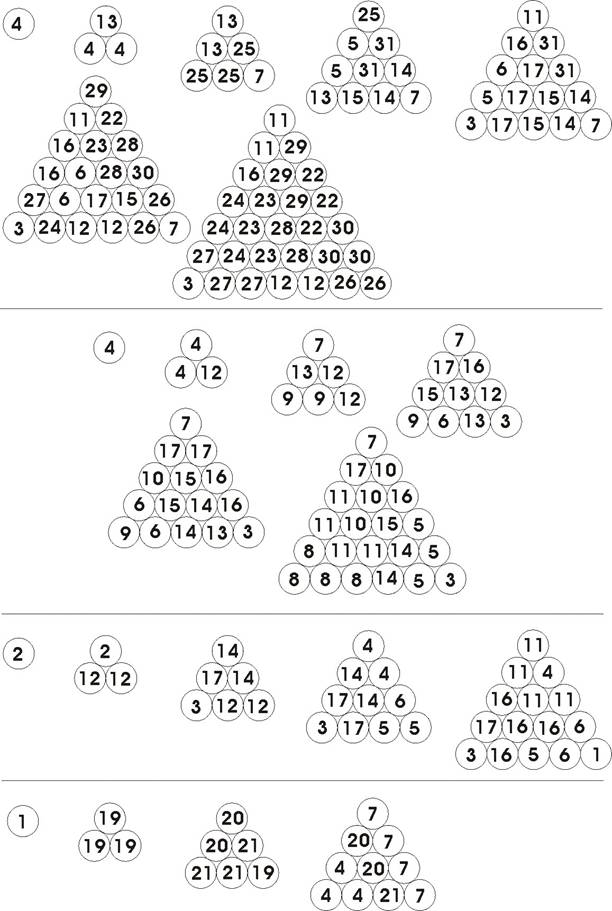
The definitions for the 3-, 4- and 5-layer cube assemblies are illustrated in the scheme of Figure 1.  The same numbers are used in turn in Figure 2 and 3 for presenting a solution for the 6-, 5- and the 4-layer cubes.  The checkering patterns of the polycubes are defined by the solutions.  Many solutions are possible for the 6 layer cube and the cubes under 4 layers [4].

 

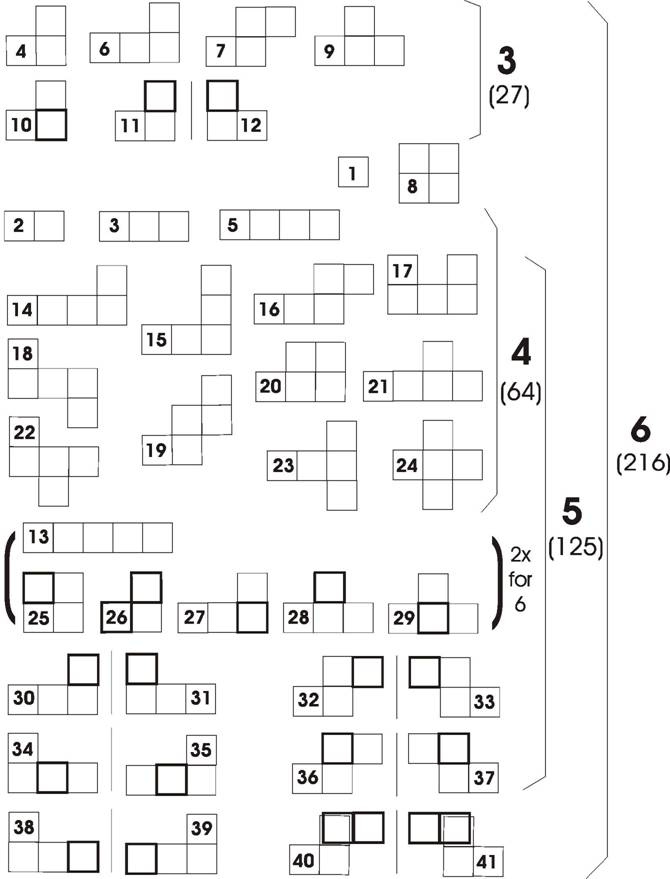
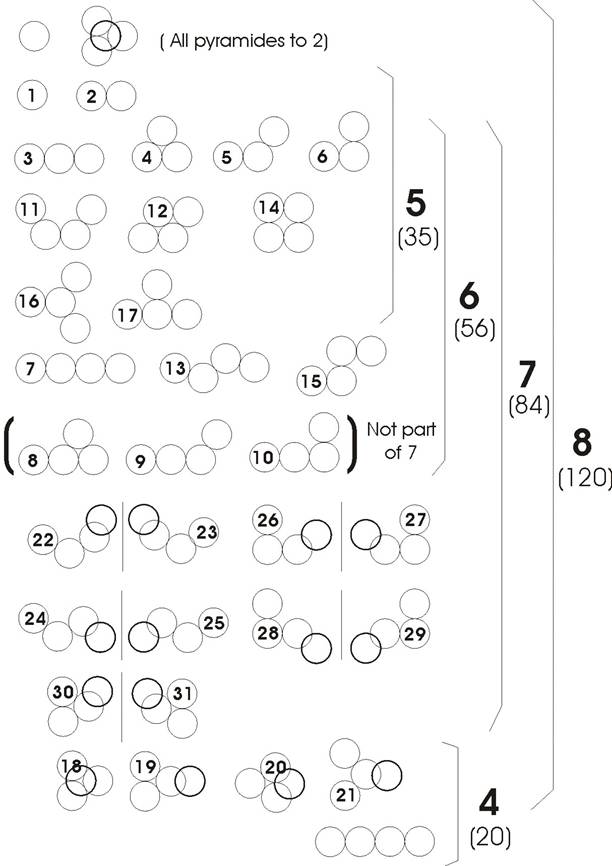
Figure 1. The poly-cubes as listed in Table 1 are shown.  Cubes presented by fine lines indicate cubes in the bottom layer, while bold stands for cubes in the upper layer.  Note that the bold cubes hide a cube in the bottom layer in all cases, except for the last two cubes of the racemes 40 and 41. Raceme pairs are indicated by lines for the mirror planes. The brackets illustrate the above definitions for the 3-, 4-, 5- and 6-layer cubes.  The total numbers of unit-cubes are also indicated, e.g. 125 cubes for the 5-layer cube.

 

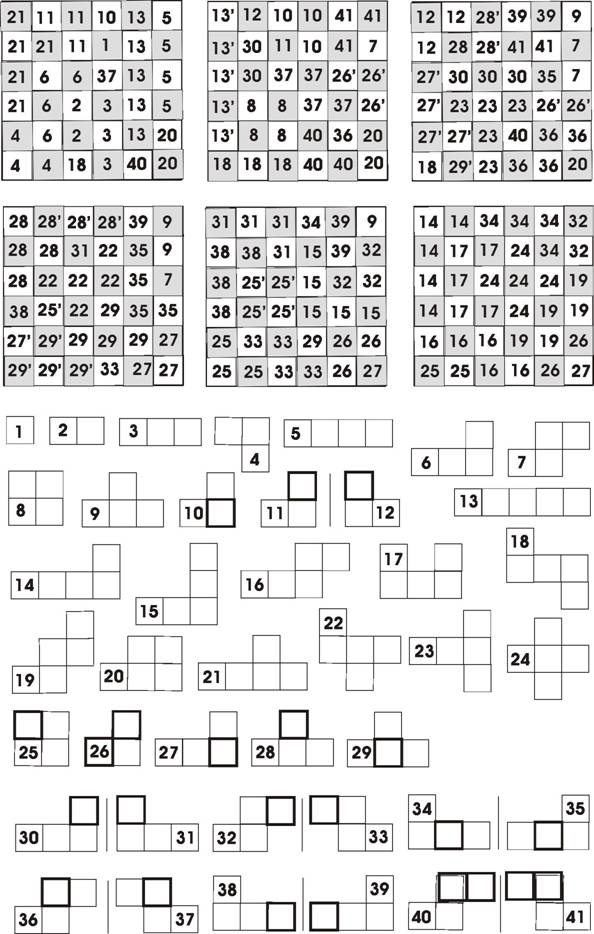
Figure 2.  Solution for the 6-layer 216-unit cube, showing the cube layers from top to bottom.  The pieces 13 and 25 to 29 are used two times and this is indicated by the primes.  For clarity all clusters are once more shown on the bottom (see Table 1 and Figure 2).  

	Figure 3.   Solutions of 4-layer, top, and 5- layer poly-cube assemblies.  The cubes are presented by layers from top down. The numbers correspond to the numbers in Table 1 and Figure 1.  The solutions for the 4- and 5-layered cubes shown define one possible coloring of the clusters.  Agreement in the coloring of all pieces is achieved for the 4-, 5- and 6-layer solutions, except for number 22 where two differently checkered individuals are needed.  A mirror image solution of the 5-layered cube would also be possible, if all raceme pairs where colored to form mirror image pairs. This condition turns out to be only fulfilled for the pair 36/37 in the solution presented.

 

 

 

Poly-ball puzzles

The crystallographic situation for the poly-ball puzzles is more complicated than in case of the poly-cubes. Only the cubic densest ball packing (layers a b c a b c...) is considered here, as a crystallographic restriction, thus excluding the hexagonal densest ball packing (layers a b a b…).  The cubic densest ball packing is the structure of metallic copper and is of point group Fm‾₃m(O⁵_h).  One possible macroscopic manifestation of this crystal structure is the famous Prussian army canon ball pyramid with its tetrahedral appearance. The three crystallographic axes are equal, orthogonal to each others and are parallel to the three four fold axis. The 3-fold axis point along <111> and there are mirror planes perpendicular to <100> and <110>. The unit cell of the face centered cubic lattice (fcc) is not a primitive unit cell as it contains 4 lattice points with 8x 1/8 + 6 x 1/2 points.

 

Each ball is surrounded by 3+6+3 balls in the triclinic direction, or by 4+4+4 balls in the cubic direction, forming 6 octahedral and 8 tetrahedral holes.  This leads to the formation of triclinic layers in the planes which are parallel to the macroscopic tetrahedron faces and cubic layers which are parallel to the opposite non-intersecting edge pairs of the tetrahedron. This is the reason why cubic (90º and 270 º) and triclinic (60 º and 300 º, 120º and 240 º) angles are intermixed in the poly-ball clusters.

 

A closer look at the buildup of the densest, or closest, ball packing reveals that the cubic (layers a b c a b c..) and hexagonal (layers a b a b…) closest packing are two fully interchangeable crystal structures. If a first plane is built up by arranging 6 balls around each ball on a flat surface, a hexagonal two-dimensional lattice is obtained (layer a).  A second layer of the same type can be added by adding balls into the dips of the first layer, by forming tetrahedron holes (layer b).  Note that placing the first ball, defines the translation vector of the second layer with respect to the first one.  Indeed every second dip stays empty. Both layers a and b are thus part of the hexagonal (hcp – P_6/mmc (D²_h) ) and the cubic closest packing (ccp – Fm‾₃m(O⁵_h) ).  The third layer can now be built by placing the first ball exactly over a ball of layer a, thus leading to the hexagonal structure abab…  Alternatively the first ball of the third layer may be placed over a tetrahedron hole of the first layer thus leading to the cubic structure abc… 

 

Note, however, that the same choice exists when building the fourth layer, thus permitting to build up sequences abab and abca, or alternatively abac and abcb, and so on. A free interchange of hcp and ccp layer sequences is thus possible and the hexagonal and the cubic structures are fully interchangeable. The packing densities of the two structures are also identical.  Note that the octahedron holes arise in the ccp structure when placing the third layer, while there are hexagonal tubes in a pure hcp crystal structure across the complete crystal.

 

The rare metals Au, Ag and Pt, for instance, crystallize in the cubic structure, like also copper.  Be, Mg, Zn, Cd, for instance crystallize in the hexagonal structure.  Cobalt can exist in either the cubic as α-Co, or hexagonal structure as  β-Co, but the layers can also freely interchange resulting in a mixed form of cobalt [9].

 

This consideration shows that in order to find out if the poly-ball clusters considered here, namely up to 4-ball assemblies, can be part of both structures we only have to test if these assemblies can be placed in up to two layers.  This is obvious for all the linear, or all of the flat pieces which contain no 90-degree angles.  All of the flat pieces which contain 90-degree angles can be placed in two layers. The same holds for all of the three-dimensional 4-ball assemblies – they can also be accommodated in just two layers.  This proves that all of the poly-ball assemblies up to tetramers can be used in both the hcp and the ccp structure. 

 

Only the tetrahedron ball pyramids are considered here and this goes beyond a limiting to cubic close packed structure for poly-ball assemblies as other macroscopic structures are possible for the face centered cubic lattice: cube, rhomb-dodecahedron, pentagon-dodecahedron, tri-tetrahedron, deltoid-dodecahedron, or tetrahedron-pentagon-dodecahedron.

 

 For convenience a trigonal 60º- coordinate system in accordance with the macroscopic tetrahedron is used to describe the puzzle assemblies, while the face centered cubic crystal lattice is aligned with the opposite non intersecting edges of the tetrahedron.  All 90º angles of poly-ball clusters are aligned with the fcc-lattice.

 

In order to define the poly-ball clusters the following nomenclature is introduced:  PB stands for Poly Ball, F is flat, T is three dimensional with a mirror plane, R are racemes or chiral pieces. Angles are 180 for straight and 60 / 300 for 60 degree, 120 /  240 for 120 degrees and 90 / 270 for right angles. Branching is indicated by y and is only introduced, if a cluster can not be described by a single continuous ball string. The maximum number of assembled balls lye on the surface and one starts with the longest straight piece.  The ball carrying the number in Figure 4 is the starting point.

 

Racemes are placed for having the maximum number of balls on the bottom surface and permitting a description with the angles ordered in the sense 30º (300º), 90º (270º), 60º (300º), and last 120º (240º).  For instance No 26 is called PB_4R_90_120 and not PB_4R_120_90. Angles are given starting with the 3^rd ball. Each ball is treated as a point for defining the symmetry. All flat pieces would otherwise have an additional mirror plane. All possible spatial positions in the cubic lattice are summed up in the position count. C2, C3, C4 stand for 2-, 3-, 4-fold symmetry axis.

 

No	Object name	Gordon notation	Position count	Mirror plane	C2	C3	C4	Point group
1	PB_1F		1	nm	n	n	n	1(C1), sphere
2	PB_2F	I2	6	2m+∞m	3xC2			mm2(C2v), mmm(D∞h)
3	PB_3F_180	I3	6	2m+∞m	3xC2			mm2(C2v), mmm(D∞h)
4	PB_3F_60	D3	8	3m+m	3xC2	1xC3		3m(C3v), ‾6m2(D3h)
5	PB_3F_120	C3	24	1m+m	1xC2			2/m(C2h), mm2(C2v)
6	PB_3F_90	L3	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
7	PB_4F_180_180	I4	6	2m+∞m	3xC2			mm2(C2v), mmm(D∞h)
8	PB_4F_180_60	P4	48	m				1(C1), m(C1h)
9	PB_4F_180_120	J4	48	m				1(C1), m(C1h)
10	PB_4F_180_90	L4	24	m				1(C1), m(C1h)
11	PB_4F_120_120	C4	24	1m+m	1xC2			2/m(C2h), mm2(C2v)
12	PB_4F_60_120	D4	12	2m+m	3xC2			mm2(C2v), mmm(D2h)
13	PB_4F_120_240	W4	24	m	1xC2			2(C2), 2/m(C2h)
14	PB_4F_90_90	O4	3	4m+m	4xC2		1xC4	4mm(C4v), 4/mmm(D4h)
15	PB_4F_90_270	S4	12	m	1xC2			2(C2), 2/m(C2h)
16	PB_4F_120y240	Y4	8	3m+m	3xC2	1xC3		3m(C3v), ‾6m2(D3h)
17	PB_4F_90y180	T4	12	1m+m	1xC2			2/m(C2h), mm2(C2v)
18	PB_4T_60_60	-	2	6m	3xC2	4xC3		23(T)
19	PB_4T_60_240	-	24	1m				m(C1h)
20	PB_4T_60_90	-	24	2m	1xC2			mm2(C2v)
21	PB_4T_90y240	-	48	1m				m(C1h)
22	PB_4R_120_120	-	24		1xC2			mm2(C2v)
23	PB_4R_240_240	-	24		1xC2			mm2(C2v)
24	PB_4R_120_240	-	24		1xC2			mm2(C2v)
25	PB_4R_240_120	-	24		1xC2			mm2(C2v)
26	PB_4R_90_120	-	24					1(C1)
27	PB_4R_270_240	-	24					1(C1)
28	PB_4R_90_240	-	24					1(C1)
29	PB_4R_270_120	-	24					1(C1)
30	PB_4R_60_90	-	24					1(C1)
31	PB_4R_300_270	-	24					1(C1)

 

Table 3.  All poly-ball clusters up to tetramers are listed. Underlined bold angles point to the second layer.  Gordon [6] named only flat poly-ball assemblies. C2, C3, C4 indicate the presence of  2-, 3-, and 4-fold symmetry axis.  The point groups of the clusters are given both with (italic) and without the mirror plane (m) parallel to the surface of the flat pieces.

 

Only clusters with mutually touching balls are considered here. Clusters which include second to nearest neighbors, using stick connections, have indeed been introduced in some puzzles [1, 2, 3, 6].  The following listing gives unique definitions for the macroscopic tetrahedral poly-ball assemblies up to the 8 layer ball pyramids:

 

- The 2 layer 4-unit ball pyramid can be built from two dimer clusters.

 

- The 3 layer ball pyramid can be built from all trimers, which do not have a 3-fold symmetry axis, plus a single ball.

 

-  The 4 layer 20-unit ball pyramid can be built from all pieces to trimers in addition to the linear 4-ball piece plus a single ball. 

 

-  More challenging, the 4 layer 20-unit ball pyramid can also be built from all, non-flat, non-raceme tetramers, in addition to the linear 4-ball piece, however, the 2-edged pyramid must be split in to the trigonal 3-ball cluster plus a single ball.

 

-  The 5 layer 35-unit ball pyramid can be built from all monomer to trimer clusters plus the non-linear flat tetramers which have at least one plane of symmetry. Note: the mirror plane parallel to the base surface of the pieces does not count.

- The 6 layer 56-unit ball pyramid can be built from all flat trimers and tetramers.

 

- The 7 layer 84-unit ball pyramid can be built from all flat 3- to 4-ball pieces which have at least one two fold symmetry axis, in addition to all raceme pieces.

-  The 8 layer 120-unit ball pyramid can be built from all parts up to tetramer clusters plus all pyramids up to the 2-layer one (the 4-ball tetrahedron plus a single ball).

 

 

            These definitions are illustrated in the scheme of Figure 3 for the 4-, 5-, 6-, 7- and 8-layer ball pyramids.  Please note that according the above definition the polymers 8, 9, and 10 are not part of the 7-layer poly-ball tetrahedron assembly.  On the other hand they are of course part of the set forming the 6-layer pyramid.  The linear tetramer is shown twice in Figure 3, as it is also part of the 4-layer pyramid.  The 8-layer 120-ball pyramid, of course contains the linear tetramer only once as indicated by the bracket.

 

Figure 5 and 6 present possible solutions for the different pyramids.  In order to permit an easier reading of these figures the various ball-polymers are once more presented in the same order as given in Table 3.  As all clusters plus the monomer only add up to 115 balls, the missing 5 balls have been brought in by adding all pyramids to 2 layers, thus considering the monomer as a one layer pyramid.  In the solution of Figure 4 these balls are indicated by 1’ and 18’ balls.  The solutions are presented by showing each layer from top to bottom.

 

Figure 6 shows the solution for the smaller ball pyramids, again according to the definitions given above.  So far no systematic searches for further solutions have been undertaken.  It is clear that the poly-ball puzzles are less restrictive than the poly-cube puzzles presented as the balls are not colored in a checkered pattern in this case.

 

 

 

 

 

 

Figure 4. The poly-balls as listed in Table 3 are shown.  All balls presented by fine lines are in the bottom layer, while bold stands for balls in the upper layer.  Raceme pairs are indicated by lines for the mirror planes. The brackets illustrate the above definitions for the 4-, 5-, 6-, 7- and 8-layer ball pyramids.  The total number of balls is also indicated, e.g. 120 balls for the 8-layer tetrahedron.

 

Figure 5.   Solution for the 8-layer 120-ball pyramid, showing the pyramid layers from top to bottom.  The pieces 1 and 18 are used two times and this is indicated by the primes.  For clarity all clusters are once more shown on the bottom. The numbers correspond to the numbers in Table 3 and Figure 3. 

 

Figure 6.   From top to bottom the solutions of the 7-, 6-, 5-, and 4-layer ball pyramids.  The numbers correspond to the numbers in Table 3 and Figure 3 and 4.   

References:

 

 

[1]      RECMATH, archive of recreational mathematics,  polypages,

          http://www.recmath.com/PolyPages/index.htm  (accessed on 18 February, 2015).

 

[2]      Kadon Enterprises, Inc. ©1998-2015 http://www.gamepuzzles.com/polycube.htm (accessed on 18 February, 2015).

 

[3]      Künzell, E. (1992). Games with Pentacubes. Heuristic Programming in Artificial Intelligence 3: the third computer olympiad (eds. H.J. van den Herik and L.V. Allis), pp.

 

[4]      Sillke, T., “Tiling and Packing results - Polycubes Problems” http://www.mathematik.uni-bielefeld.de/~sillke/results.html (accessed on 18 February, 2015).

 

[5]      Wang, H.,   He, Y.,  Li,  X. , Gu,  X.,  Qin,  H.,  Polycube Splines, Computer-Aided Design,  Elsevier,  2008.

 

[6]      Gordon, L., Chico, California, 1986. http://home.comcast.net/~gibell/puzzles/polys/Gordon_NotesOnBallPyramids3.pdf

          (accessed on 18 February, 2015).

 

[7]      Burns, G., Glazer, A.M., Space Groups for Solid State Scientist, Academic Press – Elsevier, 1971.

 

[8]      Kinsey, L.C., Moore, T. E., Prassidis, E., Geometry and Symmetry, John Wiley&Sons, 2011.

 

[9]      Kleber, W.,  Einführung in die Kristallographie, VEB Verlag Technik, Berlin 1961.

 

 

This work has been presented April, 16, 2015 by Berchtold Frank Rordorf during the XVIII Annual Colloquium of the International Society for Board Game Studies, hosted by the Swiss Museum of Games at La Tour-de-Peilz.

 

 download document in WORD for Windows:  PUBLICATION