
|
|
PUBLIKATION (existiert nur auf Englisch) |
|
DIESE PUZZLES WURDEN ENTWICKELT ALS CBT ZUR
FOEDERUNG DES VORSTELLUNGSVERMOEGENS IM 3-DIMENSIONALEN RAUM.
(COMPUTER BASED TRAINING)
Die Poly Cube (PC) and Poly Ball puzzles (PB) wurden im Jahr 2015 entwickelt und im Musée Suisse du Jeu in la Tour de Peiltz vorgestellt (bei Vevey am Geneversee in der Schweiz). Prototypen in der Form von Holzmodellen wurden an dieser Konferenz in einer Posterpresentation gezeigt. Da die Kosten der Puzzles in dieser Form viel zu hoch wären, haben wir die Puzzles mittels WEBGL (WEB Graphic Language), JAVASCRIPT und SVG (scalable vector graphics) virtualisiert. Diese Wahl der Programmiersprachen hat den Vorteil, dass diese Scriptsprachen heute sehr verbreitet sind und durch die meisten modernen Internetbrowsers interpretiert werden können. Damit werden die Puzzles Platform unabhängig und können auf den meisten Computern und Mobiltelefonen gelöst werden. Die einzelnen HTML-Files können tasächlich kopiert werden und können ohne Internetserver direkt ab einem Filesystem mit einem beliebigen WEBGL-Kompatiblen Browser geöffnet werden. Wir haben auf den Programmkode auf der Entwickler Version des MOZILA FIREFOX gebaut und auf dem Chrome-, Opera- und MS Interrnet- Explorer getestet. Dadurch wird keine APP nötig. Jeder Text Editor, so zum Beispiel der Microsoft Notepad in UTF-8 Modus, kann verwendet werden um die die Programmierung zu studieren. Natürlich kann man die Programmierung auch in den meisten Browsern betrachten durch Anklicken mit der rechten Maustaste. Persönlich entwickle ich immer noch jeglichen Code auf MS-FRONTPAGE im Zusammenspiel mit der Entwickler Version des Firefox unter Verwendung seiner WEB Konsole für die Fehlersuche. Es wurde absichtlich auf die Verwendung von INCLUDE Files verzichtet um die Transpartenz und Lesbarkeit für Studenten zu verbessern. Kommentar wurden sporadisch, also nicht mit dem Ziel einer systematischen Schulung, angebracht.
Unsere Arbeit ist auch ein praktisches Beispiel zum Inhalt des ausserordentlichen Buches WebGL Programming Guide, von K. Matsuda und R. Lea, 2015, Adison-Wesley, ISBN 978-0-321-90292-4. Die hier präsentierten Puzzles können verstanden werden als ein Computer Basierter Kurs (Computer Based Training oder CBT) zur Schulung der Vorstellungskraft und des Denkens im 3 dimensionalen Raum, eine Kompetenz die von grosser Befdeutung ist für Studenten der Naturwissenschaften, Technologie und Enginieur Wissenschaften, Architektur und nicht zuletzt fürEntwickler von 3D Spielen. Als physikalischer Chemiker bin ich voll vertraut mit der Bedeutung einer mentalen Visualisierung von Objekten im 3 dimensionalen Raum.
Zwei Arten von 3 dimensionalen Puzzles werden hier behandelt: Poly Würfel und Poly Spheren. Dabei werden grössere Objekte wie Würfel, Tetraeder oder Oktaeder aus einer Vielzahl von kleinen Polymeren zusammen gesetzt, so wie dies definiert wurde in der erwähnten Publikation. Die Puzzles in Form von Kuben sind aus Ansammlungen von Monomer bis Pentameren und die Kugel Tetraeder (3- Flächige Kugel Pyramiden) und Oktaeder sind aus Polyball Klustern von Monomeren bis Tetrameren aufgebaut. Die in den Definitionen zusammengestellten Clustergruppen erlauben es 2 bis 6 Würfel-Kantige Kuben, oder 2 bis 8 Kugel-Kantige Tetraeder zu bauen. Die Oktaeder Puzzles und die Polyball Kuben wurden erst im beiliegenden Tutorial definiert. Der kristallographische Hintergrund und damit die Mechanik der Programmierung sind viel einfacher für die Poly Würfel und sollten zuerst studiert werden, da in diesem Falle beide das Computer Bildschirm basierte Koordinatensystem und die Objekt basierten Koorfdinartensysteme, orthogonal sind. Das Rechthandige Computer Bildschirm Koordinatensystem besteht aus der horizontalen von links nach rechts wachsenden X-achse, der von unten nach oben wachsenden vertikalen y-Achse und aus der aus dem Bildschirm gegen den Betrachter zeigenden Z-Achse.
Die 2x2x2 Würfel Puzzles sind sehr einfach zu lösen aber sollten trotzdem geöffnet werden um sich mit der Benutzeroberfläche vertraut zu machen und den Translationen (Verschiebungen in x-, y-, and z- Richtung) und Rotationen (Drehungen um die x-, y-, und z-Achsen der Polymere) der einzelnen Klusters. Diese Uebungen ermöglichen es auch den Unterschied von einzelnen physischen Lösungen, wie sie in einem aus Holz zusammengestzten Polywürfel Kubus existieren, und dem im Computer virtuualisierten Equivalent, zu verstehen. Wenn wir einen aus Holz zusammen gebauten Würfel um 90 Grad rotieren, empfinden wir, dass es sich immer noch um dieselbe Lösung handelt. Im Falle der virtualisierten Lösung, haben sich alle Koordinaten und Drehwinkel der einzelnen Polymere verändert und das zugehörige JASON (Java Script Object Notation - siehe auch Store und Text) File hat sich völlig verändert. Auch die 3x3x3 Poly Würfel Puzzles sind einfach und so auch der bekannte Soma Würfel der von Piet Hein entdeckt wurde. Die grösseren Polywürfel Kuben sind schwieriger zu lösen und der von uns definierte 5x5x5 Würfel könnte eines der schwierigsten Puzzles sein, das je eingeführt wurde! Tatsächlich varbrachte ich zwei solide Monate damit eine einzige Lösung mittels Holzmodellen auf zu spüren - und dies vor der definitiven Schwarz / Weiss Einfärbung der Polymere. Der 6x6x6 Würfel ist wieder einfacher zu Vollenden, da er auch Monomere bis Trimere enthält
Uebungen an Poly Kube Gruppierungen und Beobachtung der Vervielfachung von Lösungen in Computer Virtualisierungen.
Die Uebungen mit Poly Würfeln seien vorangestellt, da wir uns hier in orthogonalen Koordinatensystemen bewegen, eine deutliche Vereinfachung im Vergleich zu den Poly Spheren. Die Uebungsziele bestehen hier aus dem Vertraut machen mit der Benutzeroberfläche, den Translationen (Verschiebungen in x-, y-, and z- Richtung) und Rotationen (Drehungen um die x-, y-, und z-Achsen der Polymere) der einzelnen Klusters, das Drehen (in 45 Grad Schritten um die y-Weltachse) und Kippen (um die x-/z-Weltachsen) der Anschauung (Welt), das lokale Speichern von Lösungen um es zu ermöglichen anlaufend den Fortschritt in der Lösungfindung ab zu Speichern, zu erfahren wie eine abgespeicherte Lösung geladen werden kann und wie eine endgültige Lösung als 2 dimensionaler Plan aufgezeigt werrden kann (MAP). Verschiedene Kluster Gruppierungen die 2x2x2 oder 3x3x3 Würfel ergeben, wurden zusammen gestellt um den Benutzer vertraut zu machen mit Klustern von zunehmender Komplexität vom Monomer zu linearen, zu flachen Klusters (PC_1F, PC_2F, PC_3F, PC_4F, PC_5F und PB_1F, PB_2F, PB_3F, PB_4F), dreidimensionalen Klusters mit Symmetrieebenen (PC_4T, PC_5T und PB_4T), und schliesslich racemischen Paaren (PC_4R, PC_5R und PB_4R) die aus gegenseitigen Spiegelbildern von 3D Klustern one interne Spiegelebenen bestehen (unsere eigenen Hände formen racemische Pärchen). Die Nomenklatur für beides die PolyKuben (PC) und PolyBällen (PB sind in Klammern angezeigt. Diese Uebunge sollen den Studenten vor allem mit der Bewegung und dem Zusammenpassen von Klustern vertraut machen.
Die Polywürfel werden Schicht um Schicht in Richtung des Beobachters aufgebaut, wobei die unterste Schicht in der vom Monitor aufgespannten XYEbene liegt. Eine fertige Lösung wird als 2D Plan dargestellt indem zuerst Align geklickt wird und anschliessend MAP ins Textfeld (genannt File) eingetypt wird und dann das Bildfeld angeklickt wird (oder als zweite Möglichkeit durch eintippen von PLAN und anschliessend MAP ins Textfeld und anklicken des Bildfeldes). Auf dem 2D Plan werden die Schichten von oben nach unten angezeigt, dh zuerst die oberste Schicht die am nächsten zum Beobachter liegt und so wird auch die Lösung des Puzzles von oben nach unten angezeigt. Auch das 3D Bild der Lösung wird von oben nach unten angezeigt und die unterste Schicht steht auf dem Monitor. Das Bild kann nach unten und nach oben gekippt werden durch wiederholtes Anklicken von TILT. Der Lösungsverbund kann auch um die vertikale y-Achse des Monitors (Welt Rotationen) gedreht werden in -90, -45, +45, 90 Grad Schritten. Der Erste Kluster ist in jedem Puzzle in roter Farbe dargestellt zur Hilfe der Orientierung. Sobald ein Kluster angewählt / aktiviert ist für translations und rotations Bewegungen, wird er farblich hervorgehoben: die erste Einheit in intensivem Gün, die zweite in Blaugrün, und die restlichen Einheiten in blassem Grün. Diese Sequenz der Einfärbung hilft dabei die Orientierung des angewählten Klusters im 3D Raum und deren Objekt orientierten x-, y-, und z-Achsen besser zu erkennen (Modellachsen Rotationen). Bei den Polywürfeln sind die möglichen Winkel aller Modellachsen Rotationen um die x-, y-, oder z-Achsen auf 90 Grad Inkremente beschränkt, also auf + oder - 90 Grad, 180 und 270 Grad.
Die folgenden einfachen Polywürfel Puzzles wurden hergestellt für das Tutorial um sich mit den komplizierteren Klustern und deren Verhalten im 3D Raum vertraut zu machen. Alle möglichen Klusters bis zu den Pentameren, inklusive einigen Doppelgängern, werden schematisch im HELP angezeigt.
Beginnen wir mit dem 2x2x2 Poly Würfel. Zuerst eine Bemerkung zur Nomenklatur: PC steht für PolyCube (PolyWürfel), PC_2x2x2 bedeutet, dass die fertige Lösung aus einem Würfel besteht deren Kantenlängen aus je 2 Einheitswürfel der konstituierenden Klustern bestehen in Richtung der x-y- und z-Achsen; cl_ gefolgt von Nummern identifiziert die Klusters die im betreffenden Puzzle enthalten sind und die im nachfolgenden HELP Kompendium aufgelistet sind. WEBGL_PC_2x2x2_cl1_2_2_4 zum Beispiel enthält die Monomer Kluster 1, 2 mal den Dimer 2 und 2bis, und schliesslich den abgewinkelten Trimer 4. Oeffnen Sie das File und versuchen Sie das sehr einfache Puzzle zu lösen indem Sie einen 2x2x2 Würfel aufbauen. Wenn sie den Würfel fertig aufgebaut haben klicken Sie Align und typen anschliessend MAP ins Textfeld um den Würfel auf dem 2D Plan zu kontrollieren. Es ist wichtig zu verstehen, dass ein grundlegender Unterschied zwischen einer physischen Lösung, aufgebaut aus einem Modell aus Holz und einer virtualisierten Lösung in einem Computer besteht: die Positionen, ausgedrückt durch die Koordinaten des ersten Würfels eines Klusters und die drei Drehwinkel um die Objektachsen x, y, und z charakterisieren jeden Kluster imComputer. Unterschiede in diesen Datensätzen können damit verschiedene Lösungen im Computer für ein und dieselbe physische Lösung vorteuschen. Als Beispiele mögen die folgenden Puzzles dienen, die nur je eine einzige physische Lösung haben: WEBGL_PC_2x2x2f_cl26, WEBGL_PC_2x2x2c_cl10, WEBGL_PC_2x2x2d_cl11, und WEBGL_PC_2x2x2e_cl12. Jeder der fertig gestellten 2x2x2 Würfel kann jedoch auf 24 verschiedene Arten plaziert werden, da jeder Würfel auf 6 verschiedenen Flächen gestellt werden kann (Unten, Oben, Links, Rechts, Vorne und Hinten) und jeder so positionierte Würfel kann weiterhin um 0, 90, 180, 270 Grad um die z-Achse gedreht werden. Dies zeigt die wichtige Tatsache, dass zwischen Holzmodell und Virtualisierung auf dem Computer ein grundlegender Unterschied besteht: für den Computer bildet jede einzelne Plazierung eine eigene Lösung mit einem eigenen Objekt Modell Matrix Stack die in JASON (JAva Script Object Notation) auslesbar ist.
Bitte öffnen Sie WEBGL_PC_2x2x2f_cl26 durch anklicken mit der rechten Maustaste in einem neuen Browser-registerblatt. Der Scroller zur Rechten vom Knopf Block zeigt bei einem ersten Oeffnen eine 1. Durch ändern dieser Einstellung zu S=Sol. und anschliessendem mit dem Mausecursor über die Bildfläche Fahren springens die 3 Kluster, bestehend aus Monomer, Dimer und dem dreidimensionalem Cluster 26 = PC_5T_90_0_90, in die einzig mögliche physische Lösung. Durch Anklicken des Align Knopfes, dann Eintippen von MAP ins Textfeld und schliesslich Anklicken der Bildfläche erscheint der 2S Plan der Lösung gefolgt von der Auflistung des Matrix Stacks der Lösung in JASON Nomenklatur auf dem html-Textfeld unterhalb der Kontrollknöpfe. Jeder einzelne Kluster ist, mit allen seinen einzelen Würfelchen, aufgelisted, jeweils mit den Koordinaten x,y,z und den 3 Modellachsen - Rotationswinkeln (Xrot, Yrot und Zrot) des ersten Würfelchens. Der Plan zeigt die Anordnung, Einfärbung und Nummer im Kluster, jedes einzelnen Würfelchens von Oben (in z-Richtung der Achse vom Monitor zum Betrachter zeigend am nächsten beim Betrachter) nach Unten (in der Ebene des Monitors liegend). Das Textfeld zeigtn in JASON Nomenklatur Dasselbe aber in der Anordnung des Matrix Stacks. Beim Anklicken des Scrollers findet man alle der 24 Positionierung der einzigen physischen Lösung die möglich ist in die html - Seite einprogrammiert, wobei die Flächen in englisch beschrieben sind (front = Vorne, back = Hinten, bottom = Unten, top = Oben, left = Links, righrt = Rechts) und die 90, 180, 270 Grad Drehungen im Urzeigersinn im rechtshandigen Koordinatensystem um die z-Achse zu verstehen sind. Durch 2-maliges Anclicken des Klusters 26 kann dieser angefärbt werden in Grün. Wenn man nun im Scroller eine andere Position anwählt bleiben alle Klusters fablich identifiziert: Rot für den Monomer, Weiss/Schaarz für den Dimer und Grün für den Tetramer. Durch Drehen und Tilten um die Weltachsen kann man so die verschdiedenen Positionierungen studieren. Ein Hinweis zum JASON Text: Align / MAP funktionieren erst für fertig aufgebaute Lösungen. Anderseits kann man jederseits eine enstehende Lösung im lokalen Browserspeicher abspeichern durch klicken auf Store und anschliessend den Matrixstack als JASON Text auslesen durch Anklicken von Text (in diesem Fall wird jeder Kluster nur einmal aufgelisted im Gegensatz zum JASON Text bei Align / MAP).
Die Tatbestände sind noch komplexer für das sehr einfache Puzzle WEBGL_PC_2x2x2a_cl8, das zwei Mal denselben zyklischen, flachen Kluster 8 verbindet. Wenn man ein Holzmodell betrachtet schaeint nur eine einzige Lösung möglich zu sein, wobei man feststellt, dass es auch eine "schlechte" Lösung gibt, bei der Schwarz neben Schwarz zu liegen kommt. Oeffnet man das File und betrachtet den Inhalt des Scrollers von oben bis unten, ann stellt man fest dass im Computer tatsächlich 8 verschiedene Lösungen möglich sind: jeder der beiden Ringe kann 4 korrekte Stellungen einnehmen, die Lösungen erlauben (0 und 180 Grad X links und rechts Drehend, für den ersten Ring, versus 90 und 270 Grad X links und rechts Drehend, für den zweiten Ring). Eine der Drehungen des ersten Rings fällt unter die Rubrik der möglichen Plazierungen der fertigen Würfel und somit sind 8 Computer Lösungen möglich und jede der 8 Lösungen kann auf 24 Arten positioniert werden. Dies bedeutet, dass für dieses Puzzle 96 verschiedene Matrix Stackes eine Lösung präsentieren können. Diese Tatsachen sind zu bedenken bei der Interpretation der Resultate von Computer Simmulationen von Lösungen! (Siehe auch Originaltext in Englisch).
Der dreidimensionale Tetramer mit Spiegelebene (WEBGL_PC_2x2x2c_cl10), das racemische Tetramer Pärchen ( WEBGL_PC_2x2x2d_cl11 und WEBGL_PC_2x2x2e_cl12 ) und nur zwei der möglichen Perntameren, nämlich 25 oder 26 ( WEBGL_PC_2x2x2f_cl26 ) können verwendet werden um 2x2x2 Polywürfwel zu bauen. Das Puzzle WEBGL_PC_2x2x2b_cl4_11 ist ein Spezialfall unter den racemischen Kluster Puzzles, da einer der beiden Kluster 11 aus dem zusammensetzbaren Monomer und dem gewinkelten Trimer aufgebaut wird und dabei eine zusätzliche Lösung im virtuellen Kontext entsteht. Zwei Kluster 10 können zu einem 2x2x2 Würfel zusammen gesetzt werden, dabei ist aber zu beachte, dass einer der Kluster umgefärbt werden muss um das Schachbrettmuster zu erhalten! Das razemische Paar das durch die Kluster 11 und 12 gebildet wird, kann nicht zu einem 2x2x2 Würfel zusammen gebaut werden. Dafür bilden aber die Lösungen der beiden Puzzles WEBGL_PC_2x2x2d_cl11 und WEBGL_PC_2x2x2e_cl12 wieder ein razemisches Paar der beiden 2x2x2 Würfel untereinander, da die beiden Würfel untereinander wieder Spiegelbilder sind.
Mehrere 3x3x3 poly Würfel Puzzles wurden erstellt um auch die restlichen drei dimensionalen Pentameren zu testen, dies in Verbindung mit einigen der flachen Klusters die über wenige interne Symmetrieelemente verfügen. Der berühmte Soma Würfel von Piet Hein gehört mit in diese Klasse. Die verschiedenen 3x3x3 Puzzles sind hervorragende Kandidaten um die Vorgehensweise beim Lösen von 3D Puzzles in virtualisierter Form zu erlernen. Es ist natürlich von Nöten intermediäre Fortschritte bei der Lösungsfindung abspeichern zu können. Dazu existieren zwei Klienten seitige Speichermethoden die ohne Internetverbindung funktionieren: Browser basierte DOM - Sessions Speicherung und Textfile Speicherung. Die erste Methode verlangt allerdingd, dass derselbe Browser zum Speichern und zum wieder Laden verwendet wird und die Daten können auf diese Weise nicht von einem auf einen andern Computer migriert werden. Der im Textfeld angezeigte Text wird dabei als Speichername verwendet und verschiedenen Vortschritte beim Suchen einer Lösung können damit gespeichert werden. Die Knöpfe Store (= Speichern), Load (= Laden) Text (= JASON Text anzeigen) und Erase (= Löschen des Speichers) un das Text Feld hinter File dienen diesem Zwecke. Zur Uebung bitte WEBGL_PC_3x3x3 oeffnen und im Scroller S=Sol. anwählen und anschliessend den Cursor über die Bildfläche bewegen so dass die Lösung erscheint. Nun das letzte Würfelchen rechts oben klicken und den Cursor nach rechts bewegen um den Kluster 6 aus dem Puzzle zu ziehen und anschliessend den Kluster nochmals anklicken um den Kluster los zu lassen und schliesslich den Store Knopf klicken. Nun den Browser neu laden oder im Scroller die Trennlinie ----- anwählen unm die Ausgangsanordnung des Puzzles wieder her zu stellen. Das Klicken des Load Knopfs bringt nun die vorher abgespeicherte Situation wieder hervor. Bitte beachten Sie, dass der Schnappschuss des Puzzles unter dem Namen eines leeren Textes abgespeichert war.
Zur Demonstration der zweiten, Browserunabhängigen, permanenteren und migrierbaren Speichermethode, klicken Sie bitte den Knopf Text und beachten, dass nun das vorher Abgespeicherte als ungeparster (kontinuierlicher Text ohne Zeilenumbrüche) JASON (JAva Script Object Notation) Textfaden erscheint, den man über Copy / Paste (Control C und Control V) in einen reinen ASCII Text Editor, wie zum Beispiel der Microsoft Notepad kopieren und im Filesystem zum Beispiel unter dem Namen LOESUNG abspeichern kann. Bitte laden Sie wieder die Ausgangssituation durch Anwählen der Trennlinie (beachten Sie dass der Scroller nur auf Aenderungen reagiert, wenn als schon ----- angewählt war, zum Beispiel auf 1 und dann wieder auf ----- stellen). Nun bitte den Browse... Knopf hinter dem Text "Load Text File:" anklicken und das vorher abgespeicherte File LOESUNG wieder öffnen und den Cursor anschliessend über die Bildfläche bewegen. Dazu noch einen wichtigen Hinweis: Vor dem Speichern von Loesungen sollt immer der Align Knopf gedrückt werden, da dadurch alle Koordinaten gerundet werden und nur der Kristallform entsprechend korrekte Winkel abgespeichert werden.
Um auf die Diskussion des Unterschieds von Lösungen und Positionen beim 2x2x2 Würfels WEBGL_PC_2x2x2a_cl8, zurück zu kommen, habe ich auf dem Internet folgendes betreffend dem Soma Würfel gefunden. Die einte Quelle spricht von 240 Lösungen für dem bekannten 3x3x3 Soma Würfel WEBGL_PC_3x3x3Soma von Piet Hein (http://puzzler.sourceforge.net/docs/polycubes.html und http://puzzler.sourceforge.net/solutions/cubes/soma-3x3x3.txt ). Anderseits findet man in http://mathworld.wolfram.com/SomaCube.html Notitz die aussagt , dass man 1'105'920 Lösungen zu erwarten hat, basierend auf Symetriebetrachtungen. Es handelt sich wohl in diesem zweiten Falle sowol um Lösungen, als auch um Positionen. Wir haben für den Some Würfel bloss zwei Lösungen einprogrammiert, aber in Anbetracht der 240 möglichen Lösungen handelt es sich nicht um ein schwierig zu lösendes Puzzle. Die folgenden 3x3x3 Puzzles wurden zusammen gestellt um sich mit der Benutzeroberfläche vertraut zu machen und gleichzeitig die racemischen Klusters, die Spiegelbild Pärchen formen, kennen zu lernen: WEBGL_PC_3x3x3, WEBGL_PC_3x3x3a_cl30_31_33_34, WEBGL_PC_3x3x3b_cl30_31_32_35, WEBGL_PC_3x3x3c_cl18_19_22_24, WEBGL_PC_3x3x3d_cl31_37_38_39, WEBGL_PC_3x3x3e_cl36_39_40_41, WEBGL_PC_3x3x3f_cl25_27_28_29_32, WEBGL_PC_3x3x3Soma. Um die Debatte um die Poly Würfel Puzzles offen zu halten habe ich einen 4x4x4-Würfel zusammen gestellt der aus allen racemischen Pentamer Klustern plus dem linearen Dimer und Trimer aufgebaut ist WEBGL_PC_4x4x4a_racemics. Als abschliessende Uebung dürfen Sie gerne eine Lösung für dieses Puzzle finden und mir die Lösung unter brordorf@gmail.com senden. Es würde mich erstaunen, wenn nicht eine Umfärbung einiger der Klusters notwendig wird um das Schachbrettmuster zu erhalten!
Steinsalz Kristalle: Verwendung derselben Klusters wie für die Poly Kuben Würfel, die hier durch Spheren ersetzt wurden.
Diesselben Puzzles wie oben beschrieben sind hier als : WEBGL_PBC_2x2x2, WEBGL_PBC_2x2x2a, WEBGL_PBC_2x2x2b, WEBGL_PBC_3x3x3, WEBGL_PBC_4x4x4, WEBGL_PBC_5x5x5, WEBGL_PBC_6x6x6. Bei der eingebauten Lösung von WEBGL_PBC_3x3x3, zum Beispiel, handelt es sich um den Kristall von NaCl. Die weissen Atome wechseln sich regelmässig gegen die schwarzen ab und bei den einen handelt es sich um die Natrium Kationen un bei den Anderen um die Chlor Anionen.
Kluster Definitionen und die Reihenfolge der Rotationen der Kluster um die Z-, Y-, und X- Achsen Modell basierten Koordinatensystem.
Der geometrichen Kontext ist um einiges komplexer bei den Poly Ball Puzzles als bei den Poly Würfeln. Die hier präsentierten Puzzles basieren auf der Kubisch Dichtesten Kugelpackung, die Schichten in Reihenfolge von abcabc... im trigonalen Koordinatensystem enthalten. Die Winkel zwischen den x, y, und z-Achsen betragen je 60 Grad in diesem Koordinatensystem. Das nachfolgende Diagram zeigt die Anordnung der überlagerten Kugeln als Funktion der Koordinaten x, y und z und zeigt drei überlagerte Schichten in z-Richtung. Solide Linien liegen in der z=0 Ebene (Schicht a), fette Linien (Schicht b) in der z=1 Ebene, und gestrichelte in der z=-1 Ebene (Schicht c). Bei Poly Kuben bleibt das orthogonale x,y,z-Koordinatensystem des Würfels mit dem orthogonalen x,y,z-Koordinaten des Monitors überlagert und damit bleiben alle Koordinaten ganzzahlige Grössen und alle Drehwinkel Multiplels von 90 Grad. Keine dieser Vorteile bleiben beim trigonalen Koordinatensystem erhalten, und alle Koordinaten müssen andauernd zwischen dem orthogonalen und dem trigonalen System hin und her berechnet werden. Eine nähere Betrachtung zeigt, dass sich die Rotationswinkel im trigonalen System tatsächlich sehr komplex verhalten. Eine weitere Komplikation basiert in der Tatsache, dass bei den Klustern der kubisch dichtesten Kugelpackung, beides trigonale (Multiple von 30 Grad), und kubische Winkel (Multiple von 90 Grad) vorkommen. Die linearen Stück, zum Breispiel, sind Mitglieder beider Systeme. Beispiele von kubischen Klustern sind unter anderen die Kluster 6, 10, 14, 15, 17. Beispiele mit beiden trigonalen und orthogonalen Winkeln sind die razemischen Paare 26 und 27, oder 28 und 29. Die nachfolgende Tabelle zeigt die Umrechnungsfaktoren von den orthogonalen Koordinaten X, Y and Z zu den trigonalen nx, ny and nz, und von den trigonalen zu den orthogonalen. Personen die sich für die JavaScript Programmierung interessieren können sich die Funktion function Align_keydown(ev, gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) auf Linien 2303 bis 2348 anschauen, wo diese Umwandlungsfaktoren imPuzzle WEBGL_PB_4x4x4 verwendet werden, nachdem per rechter Maustaste und Siehe Seiten Quellkode das Program in Textform geöffnet wurde. Diese Faktoren erscheinen auch in der Funktion function trigCoordinatesParser() auf den Linien 3658 bis 3714 und man kann dort erkennen, dass die Tetraeder Puzzles programmiert wurden im Sinne einer Pyramide die auf der xy Monitorebene steht und in positiver z Richtung zum Beobachter hin wächst.
Alle Polyball Kluster werden mit dem ersten Ball auf 0,0,0 zentriert (x=0, y=0, z=0) definiert und dem zweiten Ball immer auf 1,0,0 (x=1, y=0, z=0). Dieses System führt zu einer besonderen Bedeutung der z, y, und y Koordinaten des zweiten Balles, der nämlich die allgemeine Orientierung des Klusters im trigonalen Koordinatensystems der Kubisch dichtesten Kugelpackung definiert. Einmal so plaziert kann der Kluster durch eine reine Drehung um die x-Achse des einhergehenden Objekt Modell Koordinatensystems in die endgültige Position in der Kubisch dichtesten Kugelpackung plaziert werden. Wird nun die Rotationssequenz von Xrot, Yrot, Zrot auf Zrot, Yrot, Xrot umgestellt, wobei bei jedem Rendering alle Rotationen neu ausgeführt werden, dann ergibt sich, dass die Rotation um die x-Achse nicht mehr an die z- und y-Rotationen gekoppelt sind. Mit anderen Worten bei nicht Befolgung dieser Definitionen und Rotationssequenzen sind die Rotationen um x und y und um y und z gekoppelt, was bedeutet dass bei einer Dreung um die x-Achse auch die Drehwinkel um y und z nachkorrigiert werden müssen (was zu Gyrolocks führen und damit eine Umstellung auf den Komplexen Raum, durch Verwendung von Quanterionen, nötig machen würde). Man sollte sich diesen Mechanismus der Plazierung der Klusters immer im Bewustsein halten bei der Lösung der Puzzles und immer die zwei Ersten zwei Kugeln (die leuchtend güne und die grün-blaue) korrekt im Kristallgitter plazieren durch eine Drehen zuerst um die z-Achse (d.h. in der Monitorebene) und dann um die y-Achse (die sich natürlich bei der Drehung um z zusammen mit dem Objekt auch verstellt hat). Erst nach der präzisen Positionierung des Klusters im Kristallgitter durch Anklicken von Align sollte man beginnen den Kluster durch eine Drehung um die x-Achse vollständig im Gitter zu plazieren. Nach nochmaligem Klicken von Align, den Zustand des Vortschritts abspeichern durch Klicken von Store.
Das folgende Diagram zeigt die kubisch dichteste Kugelpackung mit allen möglichen trigonalen und kubischen Winkeln für die Drehung der Klusters in der x-y Monitorebene (Drehungen um die z-Achse und die y-Achse). 60 Grad Winkel, zum Beispiel, kommen vor wenn die zweite Kugel in den Ebenen z=+1 oder z=-1 plaziert werden. Diese Winkel werden weiter verändert durch die Winkel von 54.74 Grad zwischen Kanten und benachbarten Flächen, oder von 70.53 Grad zwischen benachbarten Flächen. Diese zusätzlichen Winkel spielen vor Allem bei der Drehung der Objekte um die x-Achse eine grosse Rolle, wenn die Kluster in der kubisch dichtesten Kugelpackun eingepasst werden. Um alle möglichen Winkel experimentell auf zu spüren wurden Lösungen von 3x3x3, 4x4x4 und 5x5x5 Kugelpyramiden systematisch verändert durch Flippen und Drehen der Pyramiden in alle möglichen Plazierungen und die dominierenden Winkel sind in der nachfolgenden Tabelle rot hervorgehoben. Da die exakte Positionierung essenziell ist für das Gelingen einer Lösung im Kontxt der kubisch dichtesten Kugelpackung, wurde ein Mechanismus entwickelt der alle Klusters in die exakten möglichen Gitterpositionen einpasst, mit scharf definierten Koordinaten und Winkeln indem man Align Knopf klickt. Erst wenn die ersten beiden Spheren korrekt im trigonalen Kristallgitter eingepasst sind wechselt man zur Drehrichtung des Klusters um die x-Achse indem man den Knopf z>x klickt der damit zu z>x wechselt. Falls die eingestellten Rotationswinkel weit entfernt sind von den erlaubten Drehwinkel in der Kugelpackung erscheint beim Anklicken von Align eine Fehlermeldung in der Form von "1 Bad trigonal orientation dX=0.5 dY=0 dZ=1 of Clust._5" . Die Einstellversuche werden von 1 bis 3 hochgezählt und man damit 3 mal versuchen den Winkel zu verbessern bevor auf 0 zurück gesetzt wird. Beachte, das dX = 0.5 zeigt an, dass versucht wurde die zweite Kugel zwischen zwei der möglichen Schichten zu platzieren!
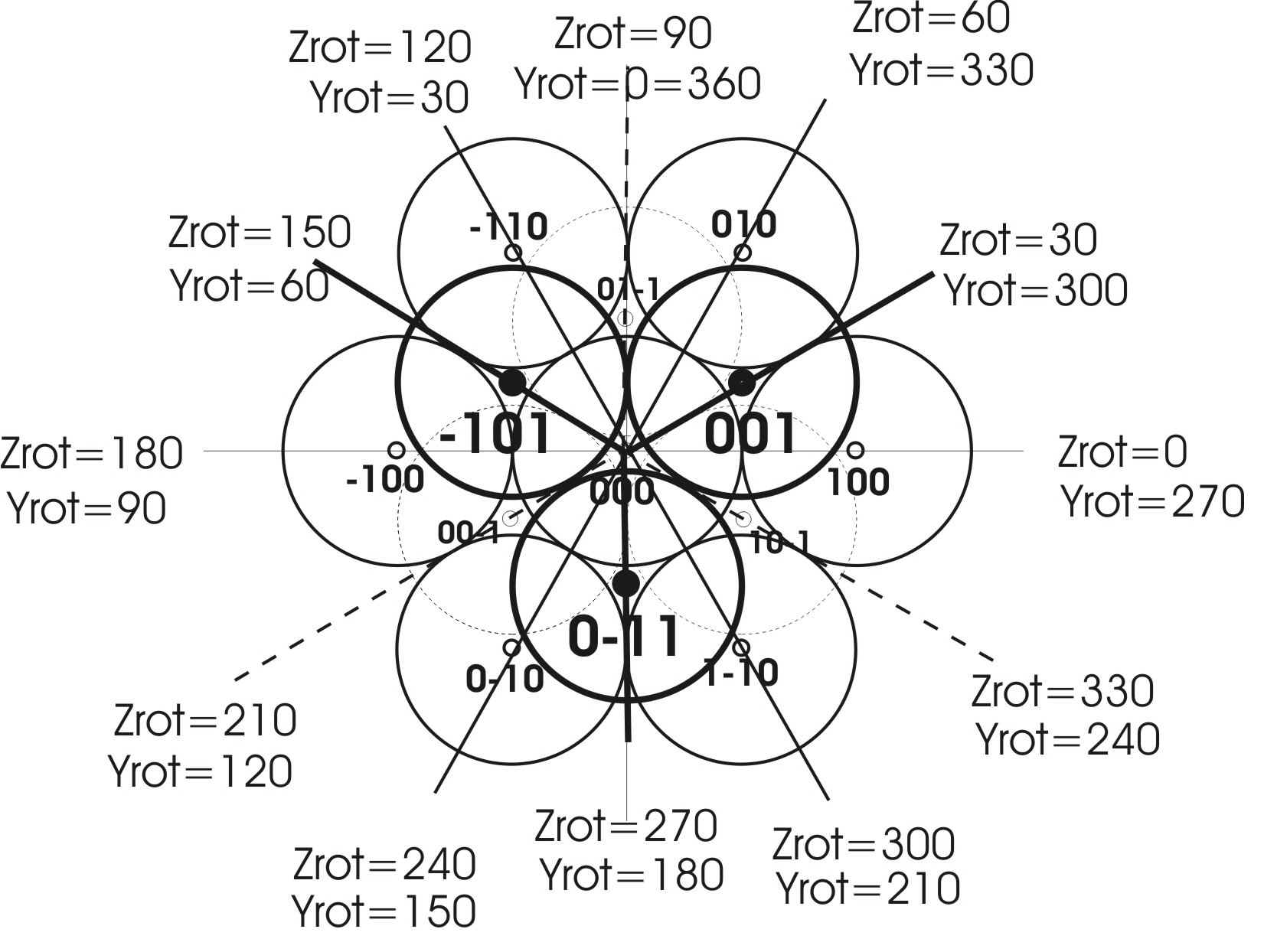
| Mögliche trigonale Winkel | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Mögliche kubische Winkel | 90 | 180 | ||||||
| Alle möglichen Winkel | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Winkel Kante-Fläche = | 54.74 | plus | 84.74 | 114.7 | 144.7 | 174.7 | 204.7 | 234.7 |
| 360 | minus | 335.3 | 5.26 | 35.26 | 65.26 | 95.26 | 125.3 | |
| Winkel Fläche-Fläche = | 70.53 | plus | 100.5 | 130.5 | 160.5 | 190.5 | 220.5 | 250.5 |
| neg + | 360 | minus | 319.5 | 349.5 | 19.47 | 49.47 | 79.47 | 109.5 |
| Alle möglichen Winkel | 210 | 240 | 270 | 300 | 330 | 360 | ||
| Winkel Kante-Fläche = | 54.74 | plus | 264.7 | 294.7 | 324.7 | 354.7 | 384.7 | 54.74 |
| minus | 155.3 | 185.3 | 215.3 | 245.3 | 275.3 | 305.3 | ||
| Winkel Fläche-Fläche = | 70.53 | plus | 280.5 | 310.5 | 340.5 | 370.5 | 400.5 | 430.5 |
| minus | 139.5 | 169.5 | 199.5 | 229.5 | 259.5 | 289.5 |
Uebungen mit Polyball Vereinigungen zwecks Familiarisierung mit der Kubisch dichtesten Kugelpackung.
Bitte oeffnen Sie das einfachste der Polyball Puzzles WEBGL_PB_2x2x2 und versuchen Sie eine 2 Ball kantige tetraedrische Kugelpyramide zu bauen indem Sie den zweiten Dimer Kluster von Rechts nach Links über die Bildfläche ziehen. Plazieren sie den grünen Ball so über dem rot-weissen Dimer dass ein Dreieck gebildet aus den roten, weissen und grünen Ball entsteht und klicken Sie Align. Nun klicken Sie den Rot (Rotate) Knopf und plazieren anschliessend die blaugrüne Kugel über dem vorher gebauten rot-weiss-grünen Dreieck (das heisst auf Sie zu kommend wenn Sie in den Monitor blicken). Klicken Sie nochmals Align und beobachten Sie wie die grünblaue Kugel in die korrekte Position hüpft um einen Tetraeder mit den anderen Kugeln zu bilden, falls Sie die blaugrüne Kugel tatsächlich über dem Dreieck plaziert haben also in positiver Richtung der z-Achse des Monitor basierten orthogonalen Koordinatensystem. Falls die blaugrüne Kugel jedoch in negativer z Richtung, das heisst unter den drei Kugeln plaziert wurden erscheint beim Klicken von Align eine Fehlermeldung im Sinne von "1 Bad trigonal orientation dX=-1 dY=1 dZ=1 of Clust._48". Dies zeigt an, dass in diesem Falle die Richtung vom grünen Ball zum blaugrünen Ball nicht kompatibel ist mit der hier verwendeten Orientierung der kubisch dichtesten Kugelpackung. Ein Blick auf das oben stehende Schema der Kugelpackung erhellt dies. Die trigonale x Achse ist kongruent zur orthogonalen, horizontalen x Achse des Monitors, die also von Linbks nach Rechts vom Ball 0,0,0 zum Ball 1,0,0 zeigt. Die trigonale y-Achse hingegen ist nicht kongruent zur y-Achse des Monitors. Sie liegt zwar immer noch in der Monitor Ebene aber zeigt nun mit einem 60 Grad anstelle des 90 Grad Winkels vom Ball 0,0,0 zum Ball 0,1,0. Die dritte Achse schliesslich, die trigonale z-Achse, zeigt in Richtung des Beobachters mit Winkeln von je 60 Grad zwischen x- und z- und zwischen y- und z- Achsen, beziehungsweise mit einem Winkel von 54.74 Grad zwischen der trigonalen z-Achse zur Monitorebene oder Grundfläche der Pyramide. Die korrekte Richtung vom grünen zum blaugrünen Ball zeigt also von 0,1,0 nach 0,0,1 , was parallel verschoben gleichbedeutend ist mit 0,0,0 nach 0,-1,1. Beachten Sie dass diese Komplikationen eine Konsequenz der Schichtabfolge von abcabc... der kubisch dichtesten Kugelpackung ist. Zusammenfassend, die Ball Pyramide ist immer oberhalb der x-Achse des Monitors zu plazieren ist so dass die trigonale x-Achse kongruent mit der Monitor x-Achse ist. Die 2x2x2 Pyramide kann natürlich auch gebaut werden indem der erste Kluster mit dem roten Ball von 0,0,0 nach 0,0,1 in z-Richtung zeigt (und jeder Dimer kann natürlich auch in die Gegenrichtung zeigen). Eine detailierte Analyse aller möglichen Trigonalpositionen wurde dokumentiert in WEBGL_PB_3x3x3TrigonalAngleAnalysis .
In der Puzzle Uebung WEBGL_PB_3x3x3 wird aus drei nicht cyclischen Trimeren eine Kugelpyramide errichtet und dies soll zeigen wie trigonale Kluster (cluster_5 = PB_3F_120) im Gegensatz zu kubischen Klustern (cluster_6 = PB_3F_90) plaziert werden. Im Folgenden eine kurze Anleitung wie eine der einprogrammierten Lösungen aufgebaut werden. Zuerst die Rote Kugel nach Links verschieben und anschliesslich denn linearen Trimer (cluster_3) mit der leuchtend grünen Kugel auf dem grünen 0,0,0 Kreuz plazieren und Align klicken. Als nächstes den rechtwinkligen Trimer (cluster_6) so dass dessen erste Kugel in der trigonalen y-Richtung über der Ersten Kugel von Kluster 6 zu liegen kommt, was die blaugrüne Kugel von Kluster 6 über der zweiten und dritten Kugel von Kluster 3 plaziert, dann Align. Nun Rot (oder Rotate) klicken und da der Kluster 6 durch die Plazierung der ersten beiden Kugeln schon korrekt in der Kugelpackung positioniert ist den Knopf z>x klicken, damit der Kluster nun um seine x-Achse gedreht werden kann. Dazu den angewählten Kluster anklicken un den Cursur gradlinig parallel zur y-Achse des Monitors nach oben verschieben was den Kluster um die x-Achse im positiven Sinn zum Drehen bringt. Für mehr Kontrolle kann man auch den x-Schieber anklicken und die rechte Cursertaste gedrückt halten bis die blassgrüne Kugel in die gewünschte Position zu liegen kommt und anschliessend Align klicken um den Kluster präzise zu plazieren. Als Nächstes Trs (oder Translate) klicken um den trigonalen Kluster (cluster_5) mit seiner ersten grünen Kugel über der ersten und zweiten Kugel des Klusters 6 plazieren (der Translate Knopf zeigt x>z an). Nach klicken des Align Knopfes, liegt der Kluster 6 immer noch ganz auf der untersten Schicht der wachsenden Kugelpyramide. Die jeweils ersten Kugeln der Kluster 3, 6 und 5 liegen nun alle auf der positven Richtung der trigonalen y-Achse mit den Koordinaten 0,0,0 , 0,1,0 und 0,2,0 (x=0, y=2, z=0).
Als Nächstes muss die zweite blaugrüne Kugel des Klusters 5 durch Rotationsbewegungen auf die trigonale Koordinatenposition 0,1,1 gebracht werden, das heisst sie muss über der ersten und zweiten Kugel von Kluster 6 zu liegen kommen. Dazu Rot (oder Rotate) klicken, mit dem Kopf für Rotation auf z>x (oder Z->X) eingestellt lassen, so dass nur Rotationen um die Zrot und Yrot Achsen mit der Maus möglich sind und die Maus bewegen um die Zrot- und Rrot- Rotationen aus zu führen, dann den Kluster anklicken. Anderseits kann der Kluster sofort angeklickt werden, was zur Statuslinien Meldung Rotate active cluster_5 auf dem Canvas führt. Diese zweite Methode befreit den Curser vom Kluster mit dem man damit zuerst den z-Schieber an klicken kann und die rechte Cursertaste niederhalten bis die blaugrüne Kugel um 90 (oder 270) Grad um die z-Achse gedreht wurde und somit die blaugrüne im Sinne der positiven y-Achse des Monitors genau über (unter) der grünen Kugel zu liegen kommt. Danach den y-Schieber anklicken und die rechte Cursortaste gedrückt halten bis die 2. Kugel von Kluster 5 über den folgenden Kugeln zu liegen kommt: 1. Kugel von Kluster 6 und 1 und 2. Kugel von Kluster 3, dann Align klicken. Nach dem Anklicken des x-Schiebers kann die 3. Kugel plaziert werden. Anderseits, kann man einen Kluster auch mit der Maus um die Modell Objekt x-Achse drehen indem man zuerst z>x (oder Z->X ) klickt. Zuerst Align klicken und dann wiederholt +45 klicken um die werdenden Pyramide um die Welt y-Achse zu drehen und sie von allen Seiten her zu sehen. Zum Schluss muss man die rote Kugel noch auf die obere Spitze der Pyramide setzen. Dazu Trs (oder Translate) klicken um von der blauen rotations zur schwarzen translations Bildfläche zurück zu kommen. Wenn man den roten Ball nach rechts schiebt verschwindet er unter der Pyramide. Um ihn nun mit der Maus nach oben (in Richtung des Beobachters) zu bewegen, muss man zuerst x>z (oder X->Z) anklicken. Man hätte statt x>z zu klicken auch das Bild zuerst 90 Grad um die Weltachse drehen können (2 mal 45+ klicken). Die dritte eleganteste Lösung um den roten Ball zu plazieren geschieht durch sein Anwählen und der Eingabe seiner trigonalen Koordinaten von 0,0,2 ins Textfeld und klicken von Align. Beachten Sie, dass wir eine zweite Lösung in Scroller vom Puzzle WEBGL_PB_3x3x3 einprogrammiert haben und dass die Kugel auf 1,0,1 sich leicht hih und her bewegt beim Umschalten zwischen den Lösungen. Dies ist eine Konsequenz von Rundungsunterschieden bei der Plazierung des kubischen Klusters cluster_6 = PB_3F_90.
Die folgenden Zusammenstellungen wurden erstellt zur Demonstration von möglichen Plazierungen der kubischen Kluster in der tetraedrischen Kugelpyramide. Bei WEBGL_PB_3x3x3a_cl7_cl10.html handelt es sich um ein Fragment einer Pyramide, und WEBGL_PB_3x3x3b_cl26_cl27 und WEBGL_PB_3x3x3c_cl30_cl31 sind interessant da hier je ein racemisches Pärchen von Klustern mit Mischungen von kubischen 90 Grad und trigonalen 60 oder 120 Grad Winkeln vorkommen. Zum Ueben im Scroller die Lösung anwählen und mit der Maus über die Bildfläche fahren. Anschliessend Align klicken und MAP ins Textfeld eingeben und die Bildfläche anklicken, so dass unter der Bildfläche der Plan der Lösungen erscheint. Nehmen Sie nun ein Screenshot der Lösung (http:hyperionics.com), wählen sie ----- in Scroller und versuchen sie die Lösung nach Plan wieder zu erstellen.
Alle der oben aufgelisteten 4x4x4 und 5x5x5 Poly Ball Puzzles wurden dazu verwendet, um für alle Kluster, die in der kubisch dichtesten Kugelpackung vorkommenden, präzisen, x-, y- und z-Drehwinkel des orthogonalen Modell Objekt basierten Koordinatensystems, zu ermitteln. Wie bei den kubischen Puzzles wurde dies durch Flippen und Drehen der Lösungen in alle möglichen Positionen bewerkstelligt. Ein Blick auf die Scroller bei den erwähnten Poly Ball Tetraedern zeigt, dass hier natürlich weniger Möglichkeiten existieren als beim Würfel und damit ist auch die Nomenklatur vereinfacht. S steht für die Lösung (Solution), R für Flippen nach Rechts, L nach Links und F nach Vorne (Front). Dies wird wieder mit den Drehwinkeln verbunden so dass sich bei je 60 Grad im Uhrzeigersinn S60cw, R60cw, L60cw, F60cw (cw = clock wise) und im Gegenuhrzeigersinn S60ccw, R60ccw, L60cw, F60ccw (ccw = counter clock wise), ergeben. Es ist zu beachten, dass es sich dabei rein um "externe" Positionierungen der Pyramidenlösungen, also der Tetraeder, handelt und nicht um "interne" Unterschiede, die sich ergeben durch symmetrie bedingte unterschiedliche Plazierungen von symmetrichen Klustern wie 4, 14, 18 und viele weiteren. Die komplete Analyse der vorkommenden Winkel kann als EXCEL Spreadsheat runter geladen werden und mit den vielen abgespeicherten Konfigurationen in WEBGL_PB_3x3x3TrigonalAngleAnalysis verglichen werden:
Download WEBGL_PB_AnglesAnalysis in EXCEL for Windows: WEBGL_PB_AnglesAnalysis.xls
Der einfache 3x3x3 Tetraeder wurde für die Winkel Analyse speziel aufgebaut
bestehend aus einer einzelnen Kugel, dem linearen Trimer, und den zwei
einfachsten nicht linearen Trimeren. Diese beiden letzten weisen entweder den
trigonalen Winkel von 120 Grad oder den orthogonalen Winkel von 90 Grad auf. Der
Vorteil des Monomers, ist dass er vollständig und unabhängig von Drehungen,
definiert wird durch seine x, y und z -Koordinaten. Auch der lineare Kluster ist
nicht beinflusst durch Rotationen um die X-Achse. Der lineare Trimer hat
gegenüber dem Dimer den Vorteil, dass die Plazierung der dritten Kugel die y-,
z-Drehwinkel mit doppelter Präzision bestimmen lässt. Der nicht linéare trigonale Kluster
lässt sich in einer der zu den den Tetraeder Flächen parallelen Ebenen plazieren.
Diese trigonalen Ebenen weisen eine sechs fache Drehsymmetrie auf. Der kubische
Kluster mit dem 90 Grad Winkel, lässt sich in einer der orthogonalen Ebenen
plazieren, die prallel liegen zu zwei sich nicht schneidenden Kanten des
Tetraeders. Diese kubischen Ebenen haben eine 4 fache Drehsymmetrie. Zwei
zusätzliche Monomerkugeln wurden bereit gestellt, als Positionierungshilfen für
die resultierende Lage der dritten Kugel der Trimeren nach den jeweiligen
Rotationen. Dieser Aufbau ermöglicht es die resultierenden korrekten Drehwinkel
der Trimeren um deren x,y und z-Achsen, nach einer Drehung des gesamten
Tetraeders einer Lösung, experimentel zu ermitteln, durch nachträgliches
austarieren eines jeden Trimers. Auf diese Weise lassen sich die realen
Drehwinkel für den "object model matrix stack" ermitteln und wir müssen uns
damit nicht mit imaginären Winkels begnügen, wie sie aus Anwendung von
Quanterionen resultieren. Beachten Sie, dass die gesamten Resultate dieser
Studie in den html-Seiten der Polyballtetraedern enthalten sind in der Funktion
Angle_combinations(i, il, Xrot, Yrot, Zrot, Xrot_ini, Yrot_ini, Zrot_ini, Rx, Ry,
Rz). Diese Funktion erlaubt es Klustervereinigungen, genannt Block, wie sie
durch fertige Lösungen entstehen, gemeinsam zu rotieren. Der Blockname 1 ist
reserviert für Vereinigungen aller Klusters die in einer gegebenen html-Seite
eingeführt wurden, und dieser Block entsteht duerch einfaches Eintypen des
Schlüsselwort LOCK ins File Textfeld. Im HELP Text wird erläutert wie ein
einzelner Kluster wieder aus einer Vereinigung heraus gelöst werden kann durch
seine Selektion und anschliessendes Anklicken des LOCK Knopfes. Im Übrigen sind
die gesamten Notizen der Winkelstudien als Kommentar am Ende Seite
WEBGL_PB_3x3x3TrigonalAngleAnalysis.html wieder gegeben.
Der LOCK Mechanismus, der es erlaubt alle Kluster einer gefundenen Lösung in
einen gemeinsamen Block zu vereinigen, erlaubt es die Lösungen in neue
Tetraederpositionen zu drehen, was natürlich zu einer Veränderung im "object
model matrix stack" führt. Dies sind komplexe Transformationen durch das
Zusammenspiel der orthogonalen Koordinatensysteme des Komputermonitores und des
Weltkoordinatensystems mit dem trigonalen Koordinatensystem der
Tetraederpyramide. Drehungen um die z-Achse sind banal mit jeweils 120-Grad
Drehungen, die jeweils neue reguläre Tetraederpositionen hervor bringen,
Positionen also, die mit dem Align Knopf präzise ausrichtbar sind. Um die
Standfläche des Tetraeders aus zu tauschen, kann der Tetraeder nach vorne (in
Richtung des Betrachters) gekippt werden, durch eine 109 Grad Drehung im
positiven Drehsinn (rechtshändiges Koordinatensystem) der x-Achse, gefolgt, zum
Beispiel, von einer positiven 60 Grad Drehung um die z-Achse. Etwas
komplizierter, kann ein solcher Austausch auch eingeleitet werden durch eine
Drehung um z, die eine Kante des Tetraeders parallel zur y-Achse bringt, gefolgt
vor einer Kippbewegung um die y-Achse um 109 oder 251 Grad. In diesem Fällen
sind also Drehsequenzen von z-Drehung, y-Drehung und z-Drehung erforderlich um
mit regulären neune Tetraederpositionen zu enden. Die Zwischenzustände des
"object model matrix stack" sollten jeweils abgespeichert und neu geladen werden
(im Browserspeicher oder im permanenten Speicher als Textfile). Diese können
natürlich nicht mittels Align ausgerichtet werden, da es sich nicht um reguläre
Tetraederpositionen handelt. Fertig ausgerichtete neue Tetraederstellungen
sollten entrigelt werden durch eintppen von UNLOCK ins Textfeld bevor einer
permanenten Speicherung, wie zum Beispiel der Einbau im Scroller durch
Javascript geübte Personen. Im übrigen sollten gedrehte Lösungen noch vor
Entriegelung (und Alignment) im Translate Modus so verschoben werden, dass die
vorderste links liegende Kugel ins grüne 0,0,0 Kreuz verschoben werden. Dies
verhindert mögliche selbstzerstörende Sprünge die während dem Align Prozess vor
kommen können, die ein Zeichen dafür sind, dass gewisse Klusters auf auf halben
Weg zwischen zwei korrekten Koordinatenpositionen zu liegen kamen.
Im Nachfolgendem ein Schritt für Schritt Verfahren zup Kippen einer
Tetraederlösung um die X-Achse: Die Lösung durch Align ausrichten, Lock ins File
Textfile schreiben, irgend einen Kluster anwählen, Block klicken, den X -
Schieber anklicken, den rechte Kursortaste betätigen bis 109 im Textfeld
erscheint. Block klicken, den Canvas 3 mal anklicken um Alles abgewählt zu haben,
Erase und Store anklicken. Irgend einen Kluster anwählen (nicht Align klicken,
da der Tetraeder sich nicht in einer regulär ausgerichteten Position befindet),
Block klicken, den Z Schieber ancklicken und mit den Kursortasten auf 60 bringen,
dann Block und schliessliche Align anklicken. Zweitens zum Kippen um die Y-Achse:
zum Beispiel die Lösung S5 im Scroller einspielen, LOCK ins Textfeld schreiben,
auf Rotate wechseln, Align klicken (dies ist wichtig da dabei die
Trigonalausrichtung eines jeden Klusters bestimmt wird), einen Kluster anwählen,
Block klicken um Blockbewegungen/-rotationen zu ermöglichen, den z-Schieber auf
330 bringen, Block klicken um die Bewegung zu beenden, Erase und Store. Refresh
klicken am Browser um die Seite neu zu laden (dies ermöglicht alle Array-Stacks
sicher zu initialisieren - Javascript hat leider keinen ArrayKill Befehl !),
Load klicken um die Zwischenlösung neu zu laden, LOCK ins Textfeld um einen
Klusterblock zu bilden, auf Rotate wechseln, Kluster anwählen (nicht Align
klicken - da wir nicht in einer regulären Tetraederposition sind!), den Y
Schieber auf 109 bringen, Block klicken, Erase udn Store. Refresh Browser, Load,
LOCK schreiben, zu Rotate umstellen, Cluster anwählen, Block klicken, Z Schieber
auf 30 bringen, Block klicken, Align klicken (wir sind nun ja wieder in einer
regulären Tetraeder Position), Erase, Store und Text. Der auf der WEB Seite
generierte Text enthält den "object model matrix stack" in JASON Nomenklatur und
kann zum permanenten Abspeichern auf einem Notepad verwendet werden(Derselbe
Textstring wird auch im Quellkode in den Lösungsscroller eingebaut innerhalb der
Quotes von var value = ''). Die umgestellte Lösung kann auch graphisch
dargestellt werden durch klicken von Align und schreiben von MAP ins Textfeld
und Canvas anklicken (Achtung allenfalls verwendete Markierungskugeln vorher aus
dem Tetraeder entfernen, durch Verschieben nach rechts - unterhalb des
Tetraeders).
Zusammenfassend ist das Verfahren zur Drehung einer Lösung in eine neue
Tetraederstellung die folgende: LOCK ins Textfeld schreiben, Align klicken, auf
Rotation umstellen, einen Kluster anwählen, Block klicken, den gewünschten
Schieber anklicken, mittels Kursortaste (< oder >) zum gewünschten Winkel fahren
and zum Abschluss Block klicken. Abschliessend sei bemerkt, dass der
Lösungscroller auch bei Refresh seinen Status beibehält und zwecks Wiederladen
einer Lösung, heraus und wieder hinein verschoben werden muss. Es kann vorkommen,
dass zur Sicherheit der Brauser abgestellt und neu geladen werden muss um Array-Leichen
zu entfernen. Noch ein Nachtrag zu den Srollers und Schiebern und deren
Eigendynamik: immer jeglichen Kluster abwählen durch drei-faches Klicken auf den
Canvashintergrund, bevor eine einschneidende Funktion wie Neuladen einer Lösung,
oder UNLOCK ausgeführt wird
Als Erstes betrachten wir die einfacheren flachen Klusters und WEBGL_PB_4x4x4a ist ein Spezialfall, da er aufgebaut ist aus fünf mal demselben P - förmigen Tetramer Kluster (cluster_8, _34, _35, _36, _37). Die Zusammenstellungen WEBGL_PB_4x4x4b und WEBGL_PB_4x4x4c waren wichtig für die Analyse der Winkel, da sie den linearen Tetramer cluster_7 enthalten, der invariant betreffend Modell Objekt x-achsen Rotationen ist, und damit die reinen z- und y- Achsen Rotationskombinationen ermitteln lässt, die in der kubisch dichtesten Kugelpackung vorkommen. Zur Uebung können Sie die Lösung von WEBGL_PB_4x4x4b öffnen und deren Plan anzeigen durch Klicken von Align, eintypen von MAP ins Textfeld und Klicken auf die Bildfläche. Kopieren Sie die Lösung auf ein Papier und zeichnen Sie die um 60 Grad im Uhrzeigersinn und im Gegenuhrzeigersinn gedrehten Lösungen. Klicken Sie ---- um das Puzzle zu initialisieren und versuchen Sie nun die von Ihnen Skizzierten Lösungen S60cw und S60ccw auf zu bauen. Versuchen Sie als Nächstes nach Laden von R die gedrehten Versionen R60cw und R60ccw direkt zu erstellen durch Verschieben (Translate) und z-, y-, z- Rotieren (Rotate) jedes einzelnen Klusters. Vergessen Sie nicht jeden Fortschritt zu Speichern durch Klicken von Align und Store. Persönlich Speichere ich oft auch durch zusätzliches Klicken von Text und Copy / Paste auf den Notepad und Speichern unter SOLUTION.txt im Foldersystem. Die Lösung kann dann wieder geladen werden durch Klicken von Browse und Aufsuchen und Öffnen des gespeicherten Textfiles. Erinnern Sie sich dass die erste grüne Kugel des Klusters plaziert (translated und rotated) werden kann durch das Eingeben von trigonalen Koordinaten (der ersten Kugel) und Rotationswinkel (des Klusters) als x,y,z,xrot,yrot,zrot ins Text feld und Klicken von Align. Zum Beispiel 0,0,3 um den linearen Kluster 7 zu plazieren in den Lösungen R, R60cw und R60ccw oder von 0,0,3,0,54.74,270 für cluster_7 in der Lösung R von WEBGL_PB_4x4x4b.
Die nächsten zwei Zusammenstellungen, WEBGL_PB_4x4x4d_cl1_4_8_9_12_16 und WEBGL_PB_4x4x4e_cl2_4_5_12_13_16 , führen den einfach zu plazierenden cluster_12 ein und cluster_16 und cluster_13 die schwieriger im Kristallgitter ein zu passen sind . Die flachen rechtwinkligen Kluster clusters_15 and _17 sind Teil der Zusammenstellung WEBGL_PB_4x4x4l_cl15_cl17. Die restlichen flachen Kluster sind Teil von WEBGL_PB_5x5x5a_cl1_3_6_7_9_10_14_15_17. Die Kluster die fünf racemische Pärchen bilden und die damit dreidimensional sind, werden in den folgenden Zusammenstellung eingeführt: WEBGL_PB_4x4x4f_cl22_cl23 und WEBGL_PB_4x4x4g_cl24_cl25 sind racemische Kluster mit trigonalen Winkeln, WEBGL_PB_4x4x4h_cl28_cl29 , WEBGL_PB_4x4x4i_cl26_cl27 und WEBGL_PB_4x4x4k_cl30_cl31, enthalten sowohl trigonale als auch orthogonale Winkel. Dreidimensionale Kluster, die interne Spiegelebenen enthalten und die damit keine racemischen Paare bilden sind mit clusters_19, _20, _21 in der Zusammenstellung WEBGL_PB_4x4x4 enthalten und der vierte dieser Klasse cluster_18 ist selber schon eine 2x2x2 tetraeder Pyramide, die einfach plazierbar ist. In einem zusammenfassenden File sind alle hier betrachteten poly Ball Klusters bis zu den Tetrameren enthalten, zusammen mit einer Anzahl von Lösungen für 4- bis 7-Ball kantige Tetraeder Pyramiden: WEBGL_PBT_4to7.
Eine ausgezeichnete Uebung um sich mit diesen Puzzles vetraut zu machen besteht schliesslich darin, zu versuchen anhand der publizierten Lösungen die 5 bis 8 schichtigen Pyramiden auf zu bauen ( WEBGL_PB_5x5x5, WEBGL_PB_6x6x6, WEBGL_PB_7x7x7 and WEBGL_PB_8x8x8 ). Beachten Sie, dass die publizierte Lösung der 7x7x7 Pyramide einen kleinen Fehler enthält: die Kugeln mit den Koordinate 004 und 024 sind vertauscht, da besetzt von cluster 13 und 25 und nicht von 25 und 13, wie publiziert.
Schritt für Schritt Anleitung für den Aufbau der tetraedrischen 8x8x8 Polyball Pyramide.
Das Folgende beschreibt in einem Schritt für Schritt Verfahren wie man die tetraedrische 8x8x8 Pyramide WEBGL_PB_8x8x8 aufbauen kann: Als Erstes die beiden überlagerten Monomere (cluster_1 und cluster_32) zur Seite schieben und dann den die erste intensiv güne Kugel von cluster_13 auf das grüne Kreuz 000 schieben (oder die trigonalen Koordinaten 0,0,0 ins Textfeld eintippen) und Align klicken. Den cluster_4 weg schieben und cluster_13 wieder anklicken, dann Rotate (oder Rot) klicken. Den Schieber z anklicken und den Kluster um + 30 Grad im Gegenuhrzeigersinn (also cw - positiv im Sinne des rechthandigen Koordinatensystems) drehen durch Drücken der rechten Cursor Taste. Dann den y - Schieber mit der Maus auf sein Maximum schieben und den Kluster durch drücken der linken Cursor Taste aufrichten in Richtung der linken ansteigenden Kante des Tetraeders (die trigonale z-Achse). Nun Align klicken und anschliessend den x Schieber mit der Maus aufs Maximum =360 Grad schieben und den Winkel um -30 Grad reduzieren durch Drücken der linken Cursor Taste und schliesslich Align klicken. Dann Translate (Trs), vor dem Speichern Text im Textfeld löschen falls solcher vorhanden ist (zum Beispiel 0,0,0), dann Erase und Store klicken. Als Nächstes cluster_4 mit seiner ersten Kugel auf Position 100 verschieben durch Eintippen von 1,0,0 ins Textfeld und Klicken von Align. Dann Rotate (oder Rot) klicken und den Kluster mit per Maus oder mit dem z Schieber um ca +30 Grad drehen und Align und Translate (oder Trs) klicken, dann Text im Textfeld löschen (persönlich speichere ich meine Fortschritte immer unter dem Namen von kein Text)und Store klicken. Zur Vergegenwärtigung aller vorhandenen Klusters mit ihrer Nummerierung HELP klicken und runter scrollen bis zur Scalable Vector Graphics (SVG) Präsentation des GLOSSARY Cluster_number <-> Cluster_names.
Als nächstes den cluster_2 nach links bewegen und durch cluster_16 ersetzen (clust_16 auf 2,0,0). Nun den Kluster 16 um +30 Grad um die z Achse drehen mit Hilfe des z Schiebers dann Align und Store klicken. Kluster 23 anwählen durch 2 mal klicken und auf die trigonale Position 4,1,0 verschieben durch Textfeld Eingabe von 4,1,0 und Klicken von Align. Dann cluster_23 um 360-120 = +240 Grad um die z Achse drehen unter Verwendung des z Schiebers und der Cursor Taste, dann Align, Translate (oder Trs), Inhalt im Textfeld löschen und Store klicken. Kluster 7 weg schieben und 8 aktivieren und auf 520 verschieben, dann Rotate (oder Rot) um +300 = 360-60 Grad um z drehen, Align, und um 180 Grad um die x Achse, Align, Translate (Trs), 5,2,0 aus dem Textfeld löschen sonst wird unter dem Namen 5,2,0 abgespeichert, und Store klicken (im Folgenden werde zwecks besserer Lesbarkeit auf das Auflisten dieser Routine Clicks verzichten). Bitte beachten Sie, dass Sie nach dem Abspeichern durch klicken von Text jederzeit die verwendeten Koordinaten und Drehwinkel kontrollieren können. Für den soeben platzierten Kluster 8 sollten sie den folgen Text finden: [8,8,"4F_180_60",0.969,0,18,5.19618,0,180,0,300, .... also Xorth=18, Yorth=5.19618,Zorth=0, Xrot=180, Yrot=0, Zrot=300, wobei es sich bei Xorth, Yorth, Zorth um die orthogonalen und nichrt die trigonalen Koordinaten handelt (Beispiel Xorth = (Xtrig +1) x 3 = (5 +1) x 3 = 18, wobei das + 1 von der Tatsache stammt, dass bei den Koordinaten ab 0 gezählt wird. Die erste Kugel des Klusters 8 befindet sich im orthogonalen Koordinatensysterm auf X = 6 x 3 und ist um 2 x 0.86603 x 3 in die y Richtung verschoben, wobei das 3 der verwendete Kugeldurchmesser ist. Siehe oben stehende Tabelle der Konversionsfaktoren). Bei komplizierten Puzzles wie diese 8x8x8 Pyramide WEBGL_PB_8x8x8, lohnt es sich den Fortschritt auch mit der permanenter Textfile Methode ab zu speichern: Nach Store , Text klicken und den JASON Text (JAva Script Object Notation) über Copy / Paste (Control C und Control V) in einen reinen ASCII Text Editor, wie zum Beispiel der Microsoft Notepad kopieren und im Filesystem zum Beispiel unter dem Namen LOESUNG abspeichern kann. Zum wieder Laden den Browse... Knopf hinter dem Text "Load Text File:" anklicken und das vorher abgespeicherte File LOESUNG wieder öffnen und den Cursor anschliessend über die Bildfläche bewegen. Dazu noch einen wichtigen Hinweis: Vor dem Speichern von Loesungen sollt immer der Align Knopf gedrückt werden, da dadurch alle Koordinaten gerundet werden und nur der Kristallform entsprechend korrekte Winkel abgespeichert werden.
Kluster 6 geht auf 4,2,0 und wird 300 Grad um die Zrot- und 54.74 Grad um die Xrot-Achse rotiert (der kubische Kluster liegt parallel zur Kante des Tetraeders und hat einen Winkel von 54.74 Grad bezüglich der Grundfläche). Kluster 20 aktivieren und auf 4,1,1 plazieren und durch eine 300 = 360-60 Grad Drehung um Zrot und um 180 Grad um Xrot in Position bringen. Kluster 31 auf Position 4,3,0 bringen und 120 Grad um z rotieren, zum Beispiel durch eintippen von 4,3,0,0,0,120 im Textfeld und klicken von Align. Kluster 22 auf 1,3,0 bringen und 300° = 360° - 60° um Zrot drehen, Align. Kluster 24 auf 0,2,0 bringen und 60°um Zrot und ungefähr 110° (109.4 Grad) um Xrot drehen, Align. Kluster 29 auf die trigonalen Koordinaten 230 setzen und 120 Grad um z drehen. Die erste Kugel von cluster_27 auf 040 bringen und durch +60 Drehung um z in seine Lage bringen. Um die Grundfläche (z = 0) zu vollenden fehlen nur noch die Kluster 15, 30 und 9. Die ersten beiden Kugeln von 30 bleiben auf der Basisfläche auf 2,4,0 und die Zrot = 60° und Xrot = 109.4°, damit kann cluster_30 durch 2,4,0,109.4,0,60 und Align plaziert werden. Kluster 30 ist schwierig zu plazieren und man sollte Uebungshalber ein bisschen mit diesem Kluster experimentieren, um all seine falschen Plazierungsmöglichkeiten in der 8x8x8 Pyramide kennen zu lernen. Kluster 15 geht auf 0,2,0 und muss 180 Grad um z und 305.26 = 360 - 54.74 Grad um y gedreht werden, da er als kubischer Kluster parallel zu einer Kante des Tetraeders eingebaut werden. Anschliessend muss der Kluster noch um 30 um die x Achse des Klusters gedreht werden (beachten sie die "horizontale" Nachbarschaft der Kugeln 15_4 und 13_4 in der dritten Schicht der 8x8x8 Pyramide). Kluster 9 geht auf die Koordinaten 070, wird um 90 Grad um z und um 234.74 = 180 + 54.74 Grad um y gedreht um die Drehachse x des Klusters im Gitter zu orientieren. Anschliessend wird Kluster 9 noch um 90 Grad um die x (Xrot im Quellcode) Achse gedreht. Bitte beachten Sie, dass all diese Winkel durch ein sorgfältiges Platzieren der Klusters im Gitter (und Klicken von Align) gefunden werden können und nicht im Textfeld eingetippt werden müssen! Der Align Mechanismus tut den Rest um approximative Winkel in präzise zu verwandeln und dies ist wichtig um eine komplexe Kugelpyramide auf bauen zu können, da sich alle Fehler über die gesamte Pyramide fortpflanzen.
Mit der Grundfläche vollendet (wiederholt +45 oder -45 klicken um die Grundfläche ze betrachten), kann man nun die zweite Schicht vollenden. Kluster 2 geht auf 1,0,1 und Zrot = 30° und Yrot = 305.26°. Der lineare Kluster 7 beginnt auf 0,0,2 und ist parallel zum Kluster 2, mit denselben Drehwinkeln. Kluster 19 wird auf 6,0,1 platziert mit Zrot = 150°, Yrot = 54.74° und Xrot = 240°. Kluster 17 beginnt auf 3,0,1 mit Zrot = 120° und Xrot = 125.26°. Der ebenfalls kubische Kluster 10 beginnt auf 2,3,1 mit Zrot = 300° und Xrot = 54.74°. Kluster 21 beginnt auf 0,4,2 (und nicht auf 2,0,2) mit Zrot = 250° und Xrot = 250.53°. Kluster 25 beginnt auf 1,3,2 mit Zrot = 300° und Xrot = 180°. Kluster 28 geht auf 1,2,3 mit Zrot = 300° und Xrot = 174.74°. Kluster 11 ist auf 2,0,2 platziert mit Zrot = 150°, Yrtot = 305.26° und Xrot = 240° was etwas schwierig ist, da der Kluster schwer sichtbar ist. In solchen Fällen kann es helfen den Kluster ausserhalb der Pyramide, zum Beispiel an der Pyramide anlehnend platziert werden um ihn dann auf die korrekten Koordinaten zu verpflanzen, hier durch eintippen von 2,0,2 und Align. 14 geht auf 3,0,3 mit Zrot = 150° und Xrot = 54.74°. Der 2x2x2 Tetraeder Kluster 18 steht auf dem Kopf mit den Koordinaten 1,1,3, mit Zrot = 270°, Yrot = 305.26° und Xrot = 54.74°. Der Monomer geht auf 0,2,3 und Kluster 5 auf 2,3,2 mit Zrot = 150°, Yrot = 305.26° und Xrot = 234.74°. Kluster 26 wird auf 2,2,3 und nicht 0,3,3 platziert mit Zrot = 330°, Yrot = 234.74° und Xrot = 54.74°. Kluster 1' ( cluster_32 = PB_1Fa) geht zu 0,2,4 und Kluster 3 auf 4,0,3 mit Zrot = 150° und Yrot = 305.26°. Der rhombische Kluster 12 geht auf 0,1,5 mit Zrot = 30° Grad und der zweite 2x2x2 Tetraeder zum Abschluss auf 0,0,6 womit die 8x8x8 Pyramide fertig gebaut ist.
POLY BALL OKTAEDER (PBO)
Einführung und Definition von Poly Ball Oktaeder Zusammenstellungen, einem weiteren Habitus der Kubisch Dichtesten Kugelpackung.
Poly Ball Oktaeder repräsentieren einen weiteren möglichen Kristallhabitus (eine mögliche makroskopische Erscheiungsform der Kristallbildung), neben dem Tetraeder oder trigonalen Pyramide, der kubisch dichtesten Kugelpackung. Puzzles dieser Form wurden in der erwähnten PUBLIKATION nicht definiert, was wir an dieser Stelle nun nachholen:
- Der 2 Ball kantige, 6-Einheiten enthaltende Poly Ball Oktaeder kann aus dem Monomer, dem Dimer und dem Trimer mit dreifacher Symmetrieachse, aufgebaut werden.
- Der 3 Ball kantige, 19-Einheiten enthaltende Poly Ball Oktaeder kann aus allen Klustern bis zum Trimer, plus dem 2-Ball kantigen Tetraeder, aufgebaut werden.
- Der 4 Ball kantige, 44-Einheiten enthaltende Poly Ball Oktaeder kann aus allen flachen Poly Ball Tetramer Klustern aufgebaut werden.
- Der 5 Ball kantige, 85-Einheiten enthaltende Poly Ball Oktaeder kann aus denselben Klustern aufgebaut werden wie die 7 Ball kantige 84-Einheiten Poly Ball Pyramide plus ein einzelner Ball. Das bedeuted aus allen flachen Trimeren und Tetrameren die mindestens eine 2-fache Simmetrieachse enthalten, und allen recemischen Klustern plus ein einzelner Ball.
- Der 6 Ball kantige, 146-Einheiten enthaltende Poly Ball Oktaeder kann aus allen Klustern bis zum Tetramer (115 Einheiten) und den nicht flachen Tetrameren die mindestens eine Symmetrieebene enthalten (16 Einheiten) plus allen Kluster bis zu den Trimeren (15 units) aufgebaut werden.
Die Kristallstruktur ist natürlich immer noch die kubisch dichteste Kugelpackung aber die möglichen Rotationswinkel haben sich verändert, da sich die Kristallstruktur relativ zum orthogonalen Koordinatensystems des Computer Monitors gedreht haben im Vergleich zum Tetraeder (der trigonalen Poly Ball Pyramide)
| Mögliche trigonale Winkel | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Mögliche kubische Winkel | 90 | 180 | ||||||
| Alle möglichen Winkel | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Winkel Kante-Fläche = | 45 | plus | 75 | 105 | 135 | 165 | 195 | 225 |
| 360 | minus | 345 | 15 | 45 | 75 | 105 | 135 | |
| Winkel Fläche-Fläche = | 54.74 | plus | 84.74 | 114.74 | 144.74 | 174.74 | 204.74 | 234.74 |
| neg + | 360 | minus | 335.26 | 5.26 | 35.26 | 65.26 | 95.26 | 125.26 |
| Alle möglichen Winke | 210 | 240 | 270 | 300 | 330 |
0=360 |
||
| Winkel Kante-Fläche = | 45 | plus | 255 | 285 | 315 | 345 | 15 | 45 |
| minus | 165 | 195 | 225 | 255 | 285 | 315 | ||
| Winkel Fläche-Fläche = | 54.74 | plus | 264.74 | 294.74 | 324.74 | 354.74 | 24.74 | 54.74 |
| minus | 155.26 | 185.26 | 215.26 | 245.26 | 275.26 | 305.26 |
| delta-ZY | Yrot | Zrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | |
| 001 | 315 | 45 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 324.74 | ||||||||||
| 001 | 225 | 225 | 90 | 144.74 | 215.26 | |||||||||||||||
| 00-1 | 135 | 45 | 35.26 | 144.74 | ||||||||||||||||
| 00-1 | 45 | 135 | 215.26 | |||||||||||||||||
| 00-1 | 45 | 225 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 324.74 | ||||||||||
| 010 | 0 | 90 | 0 | 45 | 54.74 | 125.26 | 180 | 234.74 | 305.26 | |||||||||||
| 010 | 180 | 270 | 0 | 180 | ||||||||||||||||
| 0-10 | 180 | 90 | 0 | |||||||||||||||||
| 0-10 | 0 | 270 | 0 | 45 | 54.74 | 125.26 | 180 | 234.74 | 305.26 | |||||||||||
| 01-1 | 45 | 135 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 330 | ||||||||||
| 01-1 | 135 | 315 | 0 | 35.26 | ||||||||||||||||
| 0-11 | 225 | 135 | 0 | 144.74 | 150 | 270 | ||||||||||||||
| 0-11 | 315 | 315 | 0 | 35.26 | 45 | 90 | 144.74 | 150 | 215.26 | 270 | 330 | |||||||||
| 100 | 0 | 0 | 0 | 45 | 54.74 | 120 | 125.26 | 180 | 234.74 | 305.26 | ||||||||||
| 100 | 180 | 180 | 125.26 | 180 | ||||||||||||||||
| -100 | 0 | 180 | 0 | 45 | 54.74 | 125.26 | 180 | 234.74 | 240 | 305.26 | ||||||||||
| -100 | 180 | 0 | 234.74 | |||||||||||||||||
| 1-10 | 0 | 300 | missing | |||||||||||||||||
| 1-10 | 180 | 120 | missing | |||||||||||||||||
| -110 | 0 | 120 | missing | |||||||||||||||||
| -110 | 180 | 300 | missing | |||||||||||||||||
| 10-1 | 45 | 315 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 324.74 | ||||||||||
| 10-1 | 135 | 135 | 0 | 35.26 | ||||||||||||||||
| 11-1 | 45 | 45 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 305.26 | 324.74 | |||||||||
| 11-1 | 135 | 225 | 0 | |||||||||||||||||
| -1-11 | 315 | 225 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 305.26 | 330 | |||||||||
| -1-11 | 225 | 45 | 0 | 35.26 | 144.74 | 215.26 | 330 | |||||||||||||
| -101 | 315 | 135 | 0 | 35.26 | 45 | 90 | 215.26 | 270 | 324.74 | |||||||||||
| -101 | 225 | 315 | 0 | 35.26 | 215.26 | 270 |
Die meisten der Oktaeder Puzzles die man definieren kann sind sehr schwierig zu lösende Puzzles. Tatsächlich wurde für den 4 Ball kantigen Poly Ball Oktaeder, gemäss Definition bestehend aus den 11 flachen Tetrameren, erst eine Einzige Lösung gefunden. Meine 5 Wochen andauernde Suche nach dieser einen Lösung kann anhand der 77 Austauschlösungen, die Betandteil der folgenden Zusammenstellungen sind, nachvollzogen werden. Die Austauschlösungen finden sich in der Scroller Liste der folgenden 4x4x4 Poly Ball Oktaeder Zusammenstellungen, die natürlich die Austauschkluster enthalten müssen: WEBGL_PBO_4x4x4_11x4F, WEBGL_PBO_4x4x4_11x4Fplus6x4R_26to31 , WEBGL_PBO_4x4x4_11x4Fplus1to4Fs , WEBGL_PBO_4x4x4_11x4Fplus4x4Tplus4x4R_22to25 . Alle der 77 Austauschlösungen wurden möglch durch den Austausch von mindestens einem flachen Tetramerkluster gegen einen anderen Polyball Kluster. Diese Studie wurde im gleichen Zuge dazu verwendet alle möglichen Xrot, Yrot und Zrot Drehwinkel der Kluster in den hier definierten Polyball Oktaedern zu ermitteln. Um Entwicklungszeit zu sparen wurde dies in weniger systematischer Manier als bei den Tetraedern bewältigt. Die Resultate sind in der vorher gehenden Tabelle aufgezeigt und wurden natürlich auch im Align Mechanismus für die Oktaeder eingebaut uns sind wie schon oben erwähnt einsehbar in der function drawBox(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) auf den linien 2950 bis 3676 in WEBGL_PBO_4x4x4_11x4F. .
Persönlich habe ich diese Polyballoktaeder Arbeiten als hervorragendes Werkzeug zur weiteren Schulung meiner mental-visuellen Vorstellungskraft empfunden. Ueberlegen Sie sich zum Beispiel wie der zwei Schichtige Tetraeder, Kluster Nummer 18, im Oktaeder platziert werden kann. Um die Lösungssuche zu beschleunigen habe ich mich allerdings auch eines aus 15mm Holzkugeln zusammengestellten Sets bedient. Die die 11 flachen Terameren lassen sich in maximal einer Stunde herstellen. Dies erlaubt es sehr rasch viele verschiedenen Konstellationen zu versuchen und hilft dabei eine intuitive Vertrautheit mit den Klustern zu bilden. Um Polyballoktaeder aus Holz auf zu bauen muss man sich eine invertierte egyptische Pyramide aus vier gleichseitigen Kartondreiecken bauen, die man wie ein Kaffeefilter in einen quadratischen Halter einbaut. Um diese Puzzles lösen zu können muss man sich Erstens damit vertraut machen wie die verschiedenen Kluster ins Kristallgitter eingebaut werden können. Zweitens muss man eine Strategie entwickel in der Suche der Lösungen. Dazu muss man erkennen welche Kluster einfach und möglichst unter allen Umständen im Kristallgitter zu plazieren sind. Darum sollte man vor allem die kleineren Kluster fürs Ende der Lösungssuche auf bewahren. Tatsächlich sind alle Puzzles die nur aus den grösseren Polymeren aufgebaut sind,wie etwa der 4x4x4 Polyballoktaeder, der aus den 11 flachen Tetramerklustern besteht, extrem schwierig zu lösen. Darum wurden kombinierte Zusammenstellungen vorbereitet, die es ermöglichen einen nicht mehr einpassbaren Tetramer durch einen Anderen zu ersetzen. Sie werden feststellen können, dass 77 solcher Austauschlösungen in den Scrollerlisten der verschiedenen Files der 4x4x4 Polyballoktaeder abgespeichert sind und diese dokumentieren meine lange Suche nach einer einzigen guten Lösung. Das Erste dieser Files WEBGL_PBO_4x4x4_11x4F demonstriert noch einmal in seiner Scrollerliste, wie eine einzige physische Lösung für dieses schwierige Puzzle durch Drehen ( _90, _180, _270 ) , Kippen ( S2, S3 ) und Spiegeln ( m ) zu 23 zusätzlichen Komputerlösungen führen kann
Beim Öffnen eines der oben stehenden Files findet man jeweils zwei Sammlungen von Klustern: a) die 11 flachen Tetramere die das Puzzle definieren positioniert auf der z=0 Fläche, und b) eine Ansammlung von Austauschkluster die sich auf einer Ebene bei negativem z befinden und daher kleiner erscheinen. Um einen der Austauschklusters zu verwenden muss man ihn zuerst nach >Vorne ziehen, entweder durch Eingabe der Koordinaten im Textfeld, oder durch Klicken von x>z (oder X->Z) und nach Vorne Ziehen mit der Maus oder dem z-Schieber. Das negative z ermöglicht es eine Lösung durch Align und Eintippen von MAP im Textfeld dann Anklicken der Bildfläche, korrekt als 2D SVG-Plan zu präsentieren, ohne Interferenz durch die nicht eingebauten Kluster. Probieren Sie den MAP Mechanismus indem Sie sich eine vorprogrammierte Lösung anschauen. Nach dem Laden eines Puzzle Files den Scroller zur Rechten des Knopfs Block öffnen. Wählen sie eine der einprogrammierten Lösungen und bewegen Sie den Mauscursor über die Bildfläche wodurch die Lösung in die Bildfläche springrt. Das Anwählen von der Trennlinie ----- stellt jeweils den Ausgangszustand wieder her (dabei gehen alle nicht abgspeicherten Veränderungen wieder verloren). Wenn eine Lösung geladen ist Align anklicken und mit der Tastatur MAP eintippen ins Textfeld zur Rechten des Schriftzuges File und schliesslich die Bildfläche anklicken. Damit erschein unterhalb des Kontrollfeldes der zweidimensionale Plan der Lösung und zwar Schicht um Schicht des Oktaeders von Open (positive z Werte) nach Unten (negative z Werte).
Da der ganze Komputercode OPEN ACCESS ist, kann man ihn abspeichern und in einem ASCII Texteditor editieren (ich persönlich brauche immer noch MS Frontpage) wodurch man eine eigene Lösungen fix in den Code aufnehmen kann, falls man grundlegende JavaScript Kennrtnisse hat. Suchen nach der Funktion function parseSolution() und einen neuen case einführen ( case "MySolution": ) der natürlich auch im html Teil im Scroller eingeführt werden muss in der Form von <select id="Lock_Number" size="1" value="-1"> <option value="MySolution">MySolution_inScroller</option>. Hat man also eine neue Lösung gefunden, die man mit Store abgespeichert hat und dann Text klickt, so kann man diesen Textstring per Copy / Paste in der Funktion function parseSolution() bei var value = ' '; zwischen den beiden 'Einfachquotes' einführen.
function
parseSolution()
var Solution = Lock_Number.value;
switch ( Solution ) {
case "MySolution":
var value = ' '; < Text
hier rein kopieren
break;
....
Beim Aufspühren einer Lösung musss man immer sicherstellen, dass jeder neu plazierte Kluster genau in der Kristallstruktur der kubisch dichtesten Kugelpackung eingepasst ist und dazu haben wir ein Einpass-mechanismus einprogrammiert, den man mit dem Knopf Align nach jeder Plazierungsoperation in Aktion bringt. Bevor man sich an die Polyballoktaeder Puzzles wagt sollte man sich anhand der Polyballtetraeder Beispiele einarbeiten um alle Kluster kennen zu lernen. Persönlich habe ich eine Technik entwickelt, indem ich mich existierender Kluster als Plazierungshilfe bediene. Der lineare Tetramer kann zum Beispiel als "Massstab" verwendet werden um andere Klusters zu plazieren. Noch einfacher gehts durch Eingabe der Kristallgitter - Koordinaten. Beim Aufbau eines Oktaeders starte ich beim untersten Vertex den ich in den negativen Bereich von z verlege. Für ein 4x4x4 Oktaeder, zum Beispiel verschiebe ich Kluster 7 auf die Koordinate 0,0,-3 durch Eingabe im Textfeld und klicken von Align. Dann rotiere ich den Kluster so, dass die dritte Kugel auf die Position 000 zu liegen kommt und klicke Align (wenn man umgekehrt die erste Kugel auf 0 beläst muss man den Kluster, ohne weitere Hilfe, korrekt in die Richtung einer Kante des Oktaeders rotieren). Um nun einen Kluster auf die richtige Ebene zu bringen verwende ich den Kluster 7 als Massstab und verschiebe die intensiv grünen erste Kugel des Klusters nach klicken von x>z in die gewählte Kugel von Kluster 7 und klicke Align. Anschliessend, nach klicken von z>x, verschiebe ich den Kluster in die gewünschte Position. Da die Oktaederschichten in der Ebene des Monitors orthogonal sind, vewende ich oft flache kubische Kluster, wie zum Beispiel 14 oder 15, um die neue Kluster zu plazieren. Immer sicher stellun durch klicken von Align, dass alle neu plazierten Elemente korrekt ausgerichtet sind. Sobald der Oktaeder Form annimmt, findet man immer schon plazierte Kluster um die Neulinge korrekt aus zu richten. Beachten Sie, dass eine einzige Kugel die auf der Aussenfläche des Oktaeders sichtbar bleibt, genügt einen schon korrekt ausgerichteten Kluster innerhalb des Oktaeders zu plazieren. Dies kann natürlich auch durch Eintippen der Gitterkoordinaten der ersten Kugel des Klusters getan werden. Diese Technik erlaubt es auch Plazierungsfehler zu korrigieren, die man beim Mapping (2D Plan) der Lösung entdeckt: Den betroffenen Kluster anklicken und aus dem Oktaeder raus ziehen, neu Ausrichten und wieder zurück in den Oktaeder schieben.
Als instruktive Uebung, die dazu verhilft Einblick in den Mechanismus zu erlangen, wie die Kluster ins Kristallgitter der kubisch dichtesten Kugelpackung des Oktaeders eingepasst werden, empfehle ich Ihnen zu versuchen im Detail zu verstehen, wie der folgende Drehwinkel von 35.26° zustande kommt. Um den Kluster 12 in einer der Flächen ein zu passen, die parallel zur oberen Frontfläche des Oktaeders liegen, muss er um einen Winkel von Xrot = 35.26° um die X-achse gedreht werden. Diese Xrot Rotation wird erst ausgeführt, nachdem der Kluster im Gitter schon ausgerichtet ist durch die Plazierung der ersten zwei Kugeln mit Koordinatenunterschieden von delta-X,Y,Z = 0,0,1 (was durch eine Zrot = 45° Rotation um die Z-Achse, und eine Yrot = 315° Rotation um die Y-Achse geschieht). Um den Xrot Drehwinkel verstehen zu können muss man sich die Rotationsebene vorstellen die im rechten Winkel zur Drehachse Xrot liegt. In dieser Ebene muss man sich ein rechtwinkliges Dreieck mit den bekannten Seitenlängen von S x 1/2 x √3 und S x 1/ √2 konstruieren resultierend in Bruch des Cosinus von 0.577350 (Sinus von 0.81655). Anhand der oben stehenden Tabelle kommt man somit auf den Xrot Winkel von 35.26° = 90° - 54.735610°.
Als Uebung zur Lösung dieser anspruchsvollen Puzzles empfehle ich über den Scroller eine Lösung zu laden und den zwei dimensionalen Plan ze restellen durch klicken von Align, Eintippen von MAP ins Textfeld und den Mauscursor über die Bildfläche zu bewegen. Nach Erstellen eines Screenshots im Scroller die Trennlinie ----- anwählen um die Ausgangslage zu erstellen und nun anhand des Screenshots die Lösung wieder zu erstellen. Dies erlaubt es sich mit allen Klustern vertraut zu machen und Einsicht in die Eigenheiten der Kristallstrukturen zu gewinnen. Sie werden feststellen, dass sobald die ersten beiden Kugeln (die intensiv grüne und die blau grüne) eines Klusters positioniert sind durch klicken von Align, nur noch eine Rotation um die x-Achse durch Einstellen des x-Schiebers nötig ist, um den Kluster im Gtter ein zu passen. Dasselbe betrifft auch die Rotationen um die Zrot Achse, ein Kluster kann um diese Achse gedreht werden, ohne dabei die Einstellungen der Y- und X- Rotationen zu beinflussen. Vorsicht ist geboten mit den Yrot - Rotationen, da man leicht auf eine nicht erlaubte Ausrichtung im Gitter fallen kann, mit nicht erlaubten Inkrementen der X-, Y- und Z- Koordinaten, was zu einem Reset von Xrot,Yrot,Zrot auf 0,0,0 Grad führen kann.
In der PUBLIKATION definierte Puzzles Crystallographic definitions for cube assemblies and ball-pyramid assemblies from poly-cubes and poly-balls, respectively |
|||
|
POLYCUBE WÜRFEL |
POLY BALL TETRAEDER |
POLY BALL |
POLY BALL OKTAEDER |
|
2x2x2Cube 3x3x3Cube 3x3x3Soma 4x4x4Cube 5x5x5Cube 6x6x6Cube |
3x3x3Ball 4x4x4Ball 4x4x4cBall PBT_4to7 5x5x5Ball 6x6x6Ball 7x7x7Ball 8x8x8Ball |
WEBGL_PBC_2x2x2 WEBGL_PBC_2x2x2a WEBGL_PBC_2x2x2b WEBGL_PBC_3x3x3 WEBGL_PBC_4x4x4 WEBGL_PBC_5x5x5 WEBGL_PBC_6x6x6 |
WEBGL_PBO_2x2x2 WEBGL_PBO_3x3x3 WEBGL_PBO_4x4x4 WEBGL_PBO_4x4x4_6x4R WEBGL_PBO_4x4x4_1to4Fs WEBGL_PBO_4x4x4_4x4T-4x4R WEBGL_PBO_5x5x5 |
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
HILFE und ZITATE
In allen Puzzles findet man einen HELP Knopf der eine spezifische Hilfe für die Poly Kuben oder Poly Kugel Puzzles auf englisch anzeigt. Die deutschen Uebersetzungen finden sich untenstehend für die beiden Versionen inklusive der Definitionen der Kluster. Kurze Beschreibungen der Funktionalitäten der graphischen Benutzeroberfläche sind enthalten, obwohl die meisten von ihnen durch einfaches Rumspielen mit der Oberfläche entdeckbar sein sollten. Am bestern öffnet man den einfachen 2x2x2 Polykuben Würfel um die Oberefläche zu erfahren. Unterhalb der Bildfläche befinden sich eine Ansammlung von Knöpfen und Schiebern, die die 3D Manipulationen Polykuben Kluster erlauben. Im oberen Teil der Bildfläche findet nman die wichtigsten Knöpfe un Schieber ebenfalls, um ein Spielen in VR (Viruelle Realität) zu ermöglichen durch das Verwenden von VR-Brillen und einer Maus die an das verwendete Telefon über einen "on-the-go" USB-Uebergangsstecker verbunden ist. Der erste und wichtigste Knopf Rot / Trs befindet sich ganz Links-Oben und erlaubt es zwischen den translations- (schwarze Bildfläche) und rotations- (blaue Bildfläche) Moden hin und her zu schalten.
Maus kontrollierte Verschiebungen (Translationen) oder Rotationen werden durch das Anklicken eines auserwählten Klusters ermöglicht, was sofort ersichtlich wird durch die Farbänderung des betreffenden Klusters. Bei erneutem Klicken der Maus (über dem Kluster oder der Bildfläche) wird die Bewegung eingefrohren, aber der Kluster bleibt aktiviert, was ersichtlich ist durch die weiterhin grüne Anfärbung des Klusters und der Identifikation des Klusters durch die rote Statuslinie im unteren Teil der Bildfläche. Je nach Modus zeigt es Translate active cluster n, oder Rotate active cluster n, wobei n die Kluster Nummer ist, oder nach dem ersten Klick vor jeglicher Bewegung der Maus, die Identifikation des Klusters durch Nummer und Name. Die drei Schieber, bezeichnet als X, Y und Z sind mit dem aktivierten Kluster verbunden und können ihrerseits durch anklicken ausgewählt werden und in dem Falle durch Klicken auf dem Schieber oder durch die "Cursor" Tasten verschoben werden. E>in Kluster bleibt aktiviert solange nicht auf die Bildfläche oder einen anderen Kluster geklickt wird. Bitte beachten Sie dass bei verschiedenen Brausern leicht verschiedene Reaktionen auf Interaktionen mit der Oberfläche auftreten können (siehe zum Beispiel unten den Hinweis zur Eingabe von orthogonalen Koordinaten oder Drehwinkeln im Textfeld).
Eine der Hauptprobleme mit dem Lösen von 3D Puzzles auf einem Computer, beruht auf der Tatsache, dass Computer Monitoren nur 2 Dimensional sind. Eine der drei Dimensionen ist also im Prinzip immer verzerrt oder gar unsichtbar und es ist daher wichtig die Sicht auf das Puzzle frei drehen zu können wärend dem Aufbau der Lösung. Dazu dienen die Ansichts (View:) Knöpfe +90 +45 Tilt -45 -90 die es ermöglichen die Weltansicht um plus oder minus 90 oder 45 Grad zu drehen. Schwenk (Tilt) Knopf erlaubt es rotiert die Ansicht zwischen normal ---> 45 Grad von oben ---> 45 Grad von unten ---> normal. Es ist essentiel die Ansicht andauernd zu ändern während dem Aufbau einer Lösung, damit die örtliche Lage eines jeden zu plazierenden Klusters aus allen Blickwinkeln beurteilt werden kann.
Eine wichige Hilfe zur genauen Platzierung der Kluster ist der Align Knopf der nach jeder endgültigen Verschiebung oder Rotation eines Klusters angeklickt werdcen sollte. Ein anderer wichtiger zwei Zustands Kippschalter ist der X->Z, respective Z->X Knopf der es erlaubt die horizontalen Mausbewegungen zwischen Wirkung auf X oder Z zu schalten. Bitte beachten Sie, dass die X und Z Achsen Bewegungen gekoppelt sind in den diagonalen Ansichten von 45, 135., 225, und 315 Grad Weltdrehung. Dies bedeutet, dass horizontale Mausbewegungen in diesen diagonal Positionen beide, die X und die Z Achsen, beinflussen.
Die Lock und Block Knöpfe und der Nummern (und Lösungen) Scroller ermöglichen es auserwählte Klusters in eine Gruppe (Block) von Klustern ein zu schliessen (Lock) der dann nach anklicken von Block gemeinsam verschoben, aber nicht rotiert, werden kann. Im Ganzen 5 solche Gruppierungen sind möglich und werden von 2 bis 5 mit dem Scroller eingestellt, wobei die 1 für die endgültige Lösung vorbehalten bleibt (siehe Nachfolgendes). Der Verriegelungsstatus wird auf der roten Zeile unten auf der Bildfläche angezeigt. Das eintyppen von LOCK im Textfeld erlaubt es alle Kluster (die fertige Lösung) in den Block Nummer 1 einzuriegeln. Durch eingeben von UNLOCK im Textfeld wird diese Verriegelung wieder auf gehoben.
Die letzten zwei Zeilen von Kontrollelementen erlauben es Zwischenlösungen ab zu speichern, was unerlässlich wird wenn man versucht schwierige Pzzles wie etwa den 5x5x5 oder den 6x6x6 Polywürfel auf zu bauen. Zwei verschiedene Speichermethoden wurden eingerichted: die eher flüchtige Methode der Speicherung im lokal verwendeten Browser und die aufwendigere Spreicherung der JASON Information in einem Textfile. Bitte testen sie die erste Methode, da die lokale Session Speicherung des Dokument Objekt Modells nicht mit allen Browsern funktioniert. Das Textfeld erlaubt es Filenamen einzugeben für die volatile Speichermethode. Gibt mann in diesem Feld gross geschrieben SOLUTION ein, so erscheint die einprogrammierte Lösung des Puzzles, die man im Uebrigen auch im Scroller aufsuchen kann für jedes Poly Würfel oder Poly Ball Puzzle.
Das Klicken des Store (Speichern) und anschliessend des Text Knopfes führt zur Anzeige der JASON (Java Script Object Notation) Text Version des Fortschritts der Lösung des Puzzles. Ein Anwählen und Kopieren dieses Textes inklusive der anführenden und beendenden eckigen Klammern ( von [[ bis ]] ) mittels Crl C ermöglicht ein Einfügen mittels Ctrl V in einen Text Editor, wie etwa den MS Notepad. Dieser JASON Text kann somit im Filesystem abgespeichrt werden, zum Beispiel unter den Namen 2x2x2wuerfel.txt. Auf diese weise Speichern Sie Ihre Fortschritte in der weniger volatilen, zweiten oben erwähnten, Methode ab. Den so abgespeicherten Zustand kann man jederzeit wieder zu erstellen indem man den auf den Hinweis "Import text file:" folgenen Browse Knopf klickt und das abgespeicherte Textfile im Filesystem wieder aufsucht und öffnet. Diese nicht volatile Speichermethode ist etwas komplizierter als die volatile Methode, da ein direktes Programm kontroliertes Abspeichern aus Sicherheitsgründen im Javascript verboten ist. Beachten Sie, dass diese zweite nicht volatile JASON Methode verwendet werden muss, wenn der Internet Explorer verwendet wird um im Filesystem abgespeicherte html-Seiten ab zu spielen, ausser wenn diese auf dem Lokalhost web Server installiert sind unter Inetpub/wwwroot.
Durch Eintippen von VR (Virtual Reality) ins File Text Feld und anschliessendes Klicken auf die Bildfläche erschein die doppelte VR Ansicht zur Verwendung in einer Stereobrille via ein Telefon. Bitte immer den Spielzustand abspeichern vor dem Uebergang zur Virtual Reality. Nochmaliges Eintippen von VR führt zurück zur mono Ansicht.
Da es uns ein Anliegen ist, dass der gesammte Kode in jeder html-Seite transparent einsehbar ist, haben wir auf jegliche Verwendung von Includes verzichtet. Möglichtst klassisches standart Java Script wurde verwendet im Zusammenspiel mit der um 2015 eingeführten WEBGL Version von Open Graphic Language (OpenGL). Die Puzzles laufen damit nur unter den seither eingeführten Browsern. Ich habe den Kode getested auf Mozzila Firefox, Chrome, normal und development Versionen, auf Opera und auf MS Explorer und Microsoft Edge.
Die folgenden sehr guten Bücher wurden zur Entwicklung des Kodes verwendet:
E. Angel and D. Shreiner, Interactive Computer Graphics, Pearson, 7th Ed. 2015, ISBN 10: 978-1-292-01934-5.
D. Cantor and B. Jones, WEBGL Beginners Guide, 2012, PACKT, ISBN 978-1-84969-172-7.
K. Matsuda and R. Lea, WebGL Programming Guide, 2015, Adison-Wesley, ISBN 978-0-321-90292-4
Hilfe Poly Würfel
2x2x2Cube
3x3x3Cube
3x3x3Soma
4x4x4Cube
5x5x5Cube
6x6x6Cube In allen Puzzles findet man
einen HELP Knopf der eine spezifische Hilfe für die Poly Kuben
Puzzles nur auf englisch anzeigt und hier ist die deutsche Ueabersetzung
dieses Textes. HELP View (Ansicht) Lock and Block (Verriegeln in Block) Store solutions (Speichern von Lösungen) Die letzten zwei Zeilen von
Kontrollelementen erlauben es Zwischenlösungen ab zu speichern, was unerlässlich
wird wenn man versucht schwierige Puzzles wie etwa den 5x5x5 oder den 6x6x6
Polywürfel auf zu bauen. Zwei verschiedene Speichermethoden wurden eingerichted:
die eher flüchtige Methode der Speicherung im lokal verwendeten Browser und die
aufwendigere Spreicherung der JASON Information in einem Textfile. Bitte
testen sie die erste Methode, da die lokale Session Speicherung des Dokument
Objekt Modells nicht mit allen Browsern funktioniert. Das Textfeld erlaubt
es Filenamen einzugeben für die volatile Speichermethode. Gibt mann in diesem
Feld gross geschrieben SOLUTION ein, so erscheint die
einprogrammierte Lösung des Puzzles, die man im Uebrigen auch im Scroller
aufsuchen kann für jedes Poly Würfel oder Poly Ball Puzzle. Load and Text (Laden und Text) Die folgenden sehr guten Bücher wurden zur
Entwicklung des Kodes verwendet: E. Angel and D.
Shreiner, Interactive Computer Graphics, Pearson, 7th Ed. 2015, ISBN 10:
978-1-292-01934-5. D. Cantor and B.
Jones, WEBGL Beginners Guide, 2012, PACKT, ISBN 978-1-84969-172-7. K. Matsuda and
R. Lea, WebGL Programming Guide, 2015, Adison-Wesley, ISBN 978-0-321-90292-4
Hilfe Poly Bälle
3x3x3Ball
4x4x4Ball
4x4x4PBT_4to7
5x5x5Ball
6x6x6Ball
7x7x7Ball
8x8x8Ball
In allen Puzzles findet man
einen HELP Knopf der eine spezifische Hilfe für die Poly Ball
Puzzles nur auf englisch anzeigt und hier ist die deutsche Ueabersetzung
dieses Textes. HELP View (Ansicht) Lock and Block (Verriegeln in Block) Store solutions (Speichern von Lösungen) Die letzten zwei Zeilen von
Kontrollelementen erlauben es Zwischenlösungen ab zu speichern, was unerlässlich
wird wenn man versucht schwierige Puzzles wie etwa den 4x4x4Oktaeders oder des
8x8x8Tetraeders auf zu bauen. Zwei verschiedene Speichermethoden wurden eingerichted:
die eher flüchtige Methode der Speicherung im lokal verwendeten Browser und die
aufwendigere Spreicherung der JASON Information in einem Textfile. Bitte
testen sie die erste Methode, da die lokale Session Speicherung des Dokument
Objekt Modells nicht mit allen Browsern funktioniert. Das Textfeld erlaubt
es Filenamen einzugeben für die volatile Speichermethode. Gibt mann in diesem
Feld gross geschrieben SOLUTION ein, so erscheint die
einprogrammierte Lösung des Puzzles, die man im Uebrigen auch im Scroller
aufsuchen kann für jedes Poly Würfel oder Poly Ball Puzzle. Load and Text (Laden und Text) Die folgenden sehr guten Bücher wurden zur
Entwicklung des Kodes verwendet: E. Angel and D.
Shreiner, Interactive Computer Graphics, Pearson, 7th Ed. 2015, ISBN 10:
978-1-292-01934-5. D. Cantor and B.
Jones, WEBGL Beginners Guide, 2012, PACKT, ISBN 978-1-84969-172-7. K. Matsuda and
R. Lea, WebGL Programming Guide, 2015, Adison-Wesley, ISBN 978-0-321-90292-4
Ziel des Puzzles ist das Bauen des NxNxN poly Würfel
Kubus mit N= 2, 3, 4, 5 oder 6 Würfelchen pro Kante, entsprechend dem
gewählten Puzzle. Die vordere, untere Kante liegt immer auf der
X-Achse des Monitors, womit also die unterste Ebene, des auf zu bauenden
Kubus, in der X-Y Ebene des Komputer Monitors zu liegen kommt. Da wir uns in
einem rechtshandigen Koordinatensystem befinden, wird der Kubus also Schicht
um Schicht in Z-Richtung, also in Richtung zum Betrachter hin, wachsen. Da
alle Klusters immer in Richtung der X-Achse definiert sind (erster Würfel
auf 000 und zweiter Würfel auf 100, X=1, Y=0, Z=0), ist es logisch, dass die
Rotationen um die Z- und die Y- Achsen die orthogonale Orientierung eines
jeden Klusters zur Lösung des Puzzles im kubischen Kristallgitter
definieren. Es ist daher unvermeidlich einen Kluster zuerst durch Z -Y
Rotation korrekt zu orientieren und jeden nicht linearen Kluster erst dann
um die X-Achse zu drehen um den 3ten und die folgenden Würfelchen
korrekt im Gitter zu platzieren. Als Hilfe zu Platzierung eines
Klusters im Raum können auch die orthogonalen Koordinaten des ersten
Würfelchens (intensiv gün beim aktivierten Kluster) im Textfeld eingetippt
werden: zum Beispiel 1,1,2 für X=1, Y=1 und Z=2 (Siehe unten unter
Orthogonale Koordinaten Eingabe).
Beachte: so genannte Gimbal
Verriegelung kann entstehen bei Drehungen bei denen eine der 3
Rotationsachsen in eine Andere gedreht wird durch Rotation um X-, Y- oder Z-
um + oder - 90
Grad, was zu Invertierungen oder unzugänglichen Rotationen führen kann bei
den vertikalen oder horizontalen Mausbewegungen. eine einfache Abhilfe
besteht in der Rücksetzung der auslösenden Rotation und Veränderung der
X,Y,Z - Sequenz der Rotationen und/oder Betätigen des x>z / z>x
- Knopfes. Gimbal Verriegelungen wurden in unserem Falle auf ein
minimum reduziert durch die systematische definition aller Kluster in
X-Richtung und dem Einhalten der Sequenz: zuerst die Z-Rotation, dann
die Y-Rotation und erst am Ende die X-Rotation ausführen.
Kluster
Bewegen (Moving Clusters)
Translate (= Verschieben) < - >
Rotate (=Rotieren)
Maus kontrollierte Verschiebungen (Translate)
oder Rotationen (Rotate) werden ermöglicht durch das aktivieren eines
angeklickten Klusters. Ein erneutes Klicken der Maus beendet die
Bewegung des Klusters, lässt ihn aber aktiviert, was sich durch die
Einfärbung des Klusters und die rote Statuslinie unten auf der Bildfläche,
bemerkbar macht. Letztere zeigt an Translate active cluster n
(Verschieben des aktivierten Klusters n), oder Rotate active cluster n
(Rotieren des aktivierten Klusters n), wobei n die Kluster Nummer und
Namen anzeigt. Die drei Schieber X, Y, Z sind ebenfalls aktiv in
diesem Zustand, müsse aber noch angeklickt werden, falls durch sie durch die
Cursor Tasten der Tastatur zu bedienen sind. Ein Kluster bleibt
aktiviert bis die Bildfläche oder ein anderer Kluster angeklickt wird.
Knöpfe +90 +45 Tilt (Kippen) -45 -90
erlauben es das Welt-Koordinatensystem um plus / minus 90 or 45 Grad zu
drehen.
Tilt (Kippen)
Knopf schalted die Weltansicht im
Zyklus von 45 Grad von oben, von unten, und von vorne.
Die gekippte Ansicht springt zurück zur Frontansicht sobald der
Weltansichtswinkel geändert wird. Es wird zur guten Gewohnheit während
dem Aufbaus einer Lösung die Weltansichten andauernd zu verändern wärend dem
Platzieren von Klustern.
Align (Ausrichten)
Knopf ist einer
der wichtigsten Knöpfe und dient der korrektion Ausrichtung eines neu
platzierten Klusters beim Aufbau einer Lösung.
X->Z und Z->X
ist ein anderer sehr wichtiger 2 Positionen Kippschalter X->Z
und Z->X der es erlaubt bei Verschiebung (Translate) die horizontale
Mausbewegung in X-Richtung auf Verschiebung in Z-Richtung zu verändern.
Bei Rotationen erlaubt er es die vertikale Mausbewegung von Rotation um die
Z-Achse auf Rotation um die X-Achse zu verändern. Bei den diagonalen
Weltansichten von 45, 135, 225, und 315 Grad sind die X- und Z- Bewegungen
gekoppelt, also hat die Mausbewegung einen gleichzeitigen Einfluss auf die
X- und die Z-Achse.
Knöpfe
und das daneben stehende anfangs numerische Scrollfeld erlaubt es Klusters
in Blöcke mit Namen von 1 bis 5 zu verriegeln, wobei die 1 für die
endgültigen Lösungen reserviert ist (siehe LOCK / UNLOCK). Der
Verriegelungsstatus ist auf der roten Statuslinie unten auf der Bildfläche
an gegeben. Der Sinn der Veriegelung von Klustern ist es zu erlauben
sie nach dem Anklicken von Block gemeinsam als Lösungsblock
verschieben zu können (dies ist nur im Translate und nicht im Rotate Modus
möglich). Beim Eintippen von LOCK ins File Textfeld werden alle
vorhandenen Kluster in den Block Nummer 1 verriegelt womit alle gemeinsam
verschoben werden können. Eintippen von UNLOCK entriegelt alle Kluster
wieder.
Die letzten
zwei Reihen von Kontrollen erlauben es Zwischenlösungen ab zu speichern was
essentiel wird wenn schwierige Puzzles wie etwa der 5x5x5Würfel oder der
6x6x6Würfel aufgebaut wird.
Das
Klicken des Store (Speichern) und anschliessend des Text
Knopfes führt zur Anzeige der JASON (Java Script Object Notation) Text
Version des Fortschritts der Lösung des Puzzles. Ein Anwählen und
Kopieren dieses Textes inklusive der anführenden und beendenden eckigen
Klammern ( von [[ bis ]] ) mittels Crl C
ermöglicht ein Einfügen mittels Ctrl V in einen Text Editor, wie etwa den MS
Notepad. Dieser JASON Text kann somit im Filesystem abgespeichrt
werden, zum Beispiel unter den Namen 2x2x2wuerfel.txt. Auf diese weise
Speichern Sie Ihre Fortschritte in der weniger volatilen, zweiten oben
erwähnten, Methode ab. Den so abgespeicherten Zustand kann man
jederzeit wieder zu erstellen indem man den auf den Hinweis "Import text
file:" folgenen Browse Knopf klickt und das abgespeicherte
Textfile im Filesystem wieder aufsucht und öffnet. Diese nicht
volatile Speichermethode ist etwas komplizierter als die volatile Methode,
da ein direktes Programm kontroliertes Abspeichern aus Sicherheitsgründen im
Javascript verboten ist.
Eingabe ins TEXT FELD
einer der folgenden Schlüsselwörter - und ANKLICKEN DER BILDFLÄCHE:
SOLUTION (LÖSUNG) um die Lösung ein zu spielen
VR zum
Umschalten auf Virtual Reality Ansicht für ein Mobiltelfon in Stereobrille.
Immer den Spielzustand abspeichern vor dem Uebergang zur Virtual Reality.
Nochmaliges Eintippen von VR führt zurück zur mono Ansicht.
PB und PC zum Umschalten von PolyWürfel auf Poly Ball Puzzles
(und PC für Poly Cube, um vom Poly Ball wieder auf PolyWürfel zu
schalten)
LOCK (Verriegeln) um alle vorhandenen Kluster in
einen einzigen Block Nummer 1 zwecks gemeinsamer Verschiebung zu Verriegeln.
UNLOCK (Entriegeln) um Block 1 wieder zu entriegeln.
PLAN
als Ersatz für ALIGN für den Fall, dass eine nicht ausgerichtete Stellung
gemapt werden soll (für Zwecke der Fehlersuche).
MAP zur
Erstellung einer 2D Ansicht - ist erst möglich nach Klicken von ALIGN oder
nach eintippen von PLAN.
Leeres Text Feld -- > um html Text
unterhalb der Kontrollknöpfe zu löschen. Achtung das Textfeld reagiert auf
Veränderungen (es muss etwas gelöscht werden und dann Bildfläche anklicken).
HELP -- > identisch wie Klicken von HELP Knopf.
Orthogonale Koordinaten
in der Form von 1,1,2 or 0,0,1 or 1,0,3 or 0,0,-1 ... -- >
um einen Kluster präzise zu platzieren. A) gewünschten Kluster aktivieren
durch anklicken und nochmals klicken. B) Textfeld anklicken und Koordinaten
in oben dargestellter Form von X,Y,Z (die Koordinaten gehen von 0 bis 9 und
können auch negativ gesetzt werden), C) den ALIGN Knopf klicken oder die
EINGABE Taste der Tastatur drücken, und dann D) den Mauskursor über
die Bildfläche bewegen. die Rotationsdrehwinkel können ebenfalls
eingegeben werden in der Form von
0,0,2,180,90,270, also als X,Y,Z,Xrot,Yrot,Zrot. Wenn nur Winkel
eingegegeben werden sollen ohne die position des ersten Würfels / Kugel zu
verändern, dann müssen die X,Y,Z Koordinaten leer aber Komma getrennt
eingegeben werden: ,,,180,90,270 setzt Xrot auf 180, Yrot auf 90 und Zrot
auf 270
Grad ohne die Position des Klusters zu verändern (bitte beachten zwischen
den Kommas befinden sich KEINE LEERSCHLÄGE ! ).
Achtung der MS internet Explorer ist eigenartig und ermöglicht
Koordinateneingaben mit Komma getrennten Werten nur bei Bestätigung durch
Klicken von ALIGN und nicht durch Drücken der Eingabetaste.
Da es uns
ein Anliegen ist, dass der gesammte Kode in jeder html-Seite transparent
einsehbar ist, haben wir auf jegliche Verwendung von Includes verzichtet.
Möglichtst klassisches standart Java Script wurde verwendet im Zusammenspiel
mit der um 2015 eingeführten WEBGL Version von Open Graphic Language
(OpenGL). Die Puzzles laufen damit nur unter den seither eingeführten
Browsern. Ich habe den Kode getested auf Mozzila Firefox, Chrome, normal
und development Versionen, auf Opera und auf MS Explorer und Microsoft Edge
GLOSSARY Cluster_number <-> Cluster_names
1=cluster 2=clustname
1 PC_1F
2 PC_2F
3 PC_3F_180
4 PC_3F_90
5 PC_4F_180_180
6 PC_4F_180_90
7 PC_4F_90_270
8 PC_4F_90_90
9 PC_4F_180y90
10 PC_4T_90y0
11 PC_4R_90_0
12 PC_4R_270_0
13 PC_5F_180_180_180
14 PC_5F_180_180_90
15 PC_5F_180_90_180
16 PC_5F_180_90_270
17 PC_5F_90_180_90
18 PC_5F_90_180_270
19 PC_5F_90_270_90
20 PC_5F_180_90_90
21 PC_5F_180_180y90
22 PC_5F_90y180y270
23 PC_5F_180_90y270
24 PC_5F_90y180y270
25 PC_5T_90_90_0
26 PC_5T_90_0_90 equals:
27 PC_5T_180_90y0
28 PC_5T_180y90_0
29 PC_5T_180y90y0
30 PC_5R_180_90_0
31 PC_5R_180_270_0
32 PC_5R_90_270_0
33 PC_5R_270_90_0
34 PC_5R_90_180y0
35 PC_5R_270_180y0
36 PC_5R_90_270y0
37 PC_5R_270_90y0
38 PC_5R_90_180_0
39 PC_5R_270_180_0
40 PC_5R_90_0_270
41 = 1bis PC_1Fbis
42 = 2bis PC_2Fbis
43 = reserve not used
44 = 13bis PC_5F_180_180_180bis
45 = 25bis PC_5T_90_90_0bis
46 = 26bis PC_5T_90_0_90bis
47 = 27bis PC_5T_180_90y0bis
48 = 28bis PC_5T_180y90_0bis
49 = 29bis PC_5T_180y90y0bis
Ziel des Puzzles ist das Bauen des NxNxN poly Ball
Tetraeder / Oktaeder mit N= 2, 3, 4, 5, 6, 7 oder 8 Kugeln pro Kante,
entsprechend dem gewählten Puzzle. Die vordere, untere Kante liegt
immer auf der X-Achse des Monitors, womit also die unterste Ebene, des auf
zu bauenden Tegtraeders, in der X-Y Ebene des Komputer Monitors zu liegen
kommt. Da wir uns in einem rechtshandigen Koordinatensystem befinden,
wird der Tetraeder also Schicht um Schicht in Z-Richtung, also in Richtung
zum Betrachter hin, wachsen. Beim Oktaeder liegt die grösste, mittlere
Fläche im Monitor und die unterste Ebene ist im negativen Z-Bereich, also
hinter dem Monitor. Die Ebenen des Oktaeders über der mittleren Ebene liegen
damit im positiven Z-Bereich, als in Richtung des Beobachters. Da alle
Klusters immer in Richtung der X-Achse definiert sind (erster Ball auf 000
und zweiter Ball auf 100, X=1, Y=0, Z=0), ist es logisch, dass die
Rotationen um die Z- und die Y- Achsen die trigonale Orientierung eines
jeden Klusters zur Lösung des Puzzles in der kubisch dichtesten Kugelpackung
definieren. Es ist daher unvermeidlich einen Kluster zuerst durch Z -Y
Rotation korrekt zu orientieren und jeden nicht linearen Kluster erst
anschliessend um die X-Achse zu drehen mit dem Ziel die 3te und die
folgenden Kugeln korrekt im Kristallgitter zu platzieren. Als Hilfe zu
Platzierung eines Klusters im Raum können auch die trigonalen Koordinaten
der ersten Kugel (intensiv gün beim aktivierten Kluster) im Textfeld
eingetippt werden: zum Beispiel 1,1,2 für Xtrig=1, Ytrig=1 und Ztrig=2
(Siehe unten unter trigonale Koordinaten Eingaben).
Beachte: so
genannte Gimbal Verriegelung kann entstehen bei Drehungen bei denen eine der
3 Rotationsachsen in eine Andere gedreht wird durch Rotation um X-, Y- oder
Z- um + oder - 90
Grad, was zu Invertierungen oder unzugänglichen Rotationen führen kann bei
den vertikalen oder horizontalen Mausbewegungen. eine einfache Abhilfe
besteht in der Rücksetzung der auslösenden Rotation und Veränderung der
X,Y,Z - Sequenz der Rotationen und/oder Betätigen des x>z / z>x
- Knopfes. Gimbal Verriegelungen wurden in unserem Falle auf ein
minimum reduziert durch die systematische definition aller Kluster in
X-Richtung und dem Einhalten der Sequenz: zuerst die Z-Rotation, dann
die Y-Rotation und erst am Ende die X-Rotation ausführen.
Kluster
Bewegen (Moving Clusters)
Translate (= Verschieben) < - >
Rotate (=Rotieren)
Maus kontrollierte Verschiebungen (Translate)
oder Rotationen (Rotate) werden ermöglicht durch das aktivieren eines
angeklickten Klusters. Ein erneutes Klicken der Maus beendet die
Bewegung des Klusters, lässt ihn aber aktiviert, was sich durch die
Einfärbung des Klusters und die rote Statuslinie unten auf der Bildfläche,
bemerkbar macht. Letztere zeigt an Translate active cluster n
(Verschieben des aktivierten Klusters n), oder Rotate active cluster n
(Rotieren des aktivierten Klusters n), wobei n die Kluster Nummer und
Namen anzeigt. Die drei Schieber X, Y, Z sind ebenfalls aktiv in
diesem Zustand, müsse aber noch angeklickt werden, falls durch sie durch die
Cursor Tasten der Tastatur zu bedienen sind. Ein Kluster bleibt
aktiviert bis die Bildfläche oder ein anderer Kluster angeklickt wird.
Knöpfe +90 +45 Tilt (Kippen) -45 -90
erlauben es das Welt-Koordinatensystem um plus / minus 90 or 45 Grad zu
drehen.
Tilt (Kippen)
Knopf schalted die Weltansicht im
Zyklus von 45 Grad von oben, von unten, und von vorne.
Die gekippte Ansicht springt zurück zur Frontansicht sobald der
Weltansichtswinkel geändert wird. Es wird zur guten Gewohnheit während
dem Aufbaus einer Lösung die Weltansichten andauernd zu verändern wärend dem
Platzieren von Klustern.
Align (Ausrichten)
Knopf ist einer
der wichtigsten Knöpfe und dient der korrektion Ausrichtung eines neu
platzierten Klusters beim Aufbau einer Lösung.
X->Z und Z->X
ist ein anderer sehr wichtiger 2 Positionen Kippschalter X->Z
und Z->X der es erlaubt bei Verschiebung (Translate) die horizontale
Mausbewegung in X-Richtung auf Verschiebung in Z-Richtung zu verändern.
Bei Rotationen erlaubt er es die vertikale Mausbewegung von Rotation um die
Z-Achse auf Rotation um die X-Achse zu verändern. Bei den diagonalen
Weltansichten von 45, 135, 225, und 315 Grad sind die X- und Z- Bewegungen
gekoppelt, also hat die Mausbewegung einen gleichzeitigen Einfluss auf die
X- und die Z-Achse.
Knöpfe
und das daneben stehende anfangs numerische Scrollfeld erlaubt es Klusters
in Blöcke mit Namen von 1 bis 5 zu verriegeln, wobei die 1 für die
endgültigen Lösungen reserviert ist (siehe LOCK / UNLOCK). Der
Verriegelungsstatus ist auf der roten Statuslinie unten auf der Bildfläche
an gegeben. Der Sinn der Veriegelung von Klustern ist es zu erlauben
sie nach dem Anklicken von Block gemeinsam als Lösungsblock
verschieben zu können (dies ist nur im Translate und nicht im Rotate Modus
möglich). Beim Eintippen von LOCK ins File Textfeld werden alle
vorhandenen Kluster in den Block Nummer 1 verriegelt womit alle gemeinsam
verschoben werden können. Eintippen von UNLOCK entriegelt alle Kluster
wieder.
Die letzten
zwei Reihen von Kontrollen erlauben es Zwischenlösungen ab zu speichern was
essentiel wird wenn schwierige Puzzles wie etwa des 4x4x4Oktaeders oder des
8x8x8Tetraeders aufgebaut wird.
Das
Klicken des Store (Speichern) und anschliessend des Text
Knopfes führt zur Anzeige der JASON (Java Script Object Notation) Text
Version des Fortschritts der Lösung des Puzzles. Ein Anwählen und
Kopieren dieses Textes inklusive der anführenden und beendenden eckigen
Klammern ( von [[ bis ]] ) mittels Crl C
ermöglicht ein Einfügen mittels Ctrl V in einen Text Editor, wie etwa den MS
Notepad. Dieser JASON Text kann somit im Filesystem abgespeichrt
werden, zum Beispiel unter den Namen 4x4x4PBOctaeder.txt. Auf diese
weise Speichern Sie Ihre Fortschritte in der weniger volatilen, zweiten oben
erwähnten, Methode ab. Den so abgespeicherten Zustand kann man
jederzeit wieder zu erstellen indem man den auf den Hinweis "Import text
file:" folgenen Browse Knopf klickt und das abgespeicherte
Textfile im Filesystem wieder aufsucht und öffnet. Diese nicht
volatile Speichermethode ist etwas komplizierter als die volatile Methode,
da ein direktes Programm kontroliertes Abspeichern aus Sicherheitsgründen im
Javascript verboten ist.
Eingabe ins TEXT FELD
einer der folgenden Schlüsselwörter - und ANKLICKEN DER BILDFLÄCHE:
SOLUTION (LÖSUNG) um die Lösung ein zu spielen
VR zum
Umschalten auf Virtual Reality Ansicht für ein Mobiltelfon in Stereobrille.
Immer den Spielzustand abspeichern vor dem Uebergang zur Virtual Reality.
Nochmaliges Eintippen von VR führt zurück zur mono Ansicht.
LOCK (Verriegeln) um alle vorhandenen Kluster in einen einzigen Block
Nummer 1 zwecks gemeinsamer Verschiebung zu Verriegeln.
UNLOCK
(Entriegeln) um Block 1 wieder zu entriegeln.
PLAN als Ersatz
für ALIGN für den Fall, dass eine nicht ausgerichtete Stellung gemapt werden
soll (für Zwecke der Fehlersuche).
MAP zur Erstellung einer 2D
Ansicht - ist erst möglich nach Klicken von ALIGN oder nach eintippen von
PLAN.
Leeres Text Feld -- > um html Text unterhalb der
Kontrollknöpfe zu löschen. Achtung das Textfeld reagiert auf Veränderungen
(es muss etwas gelöscht werden und dann Bildfläche anklicken).
HELP
-- > identisch wie Klicken von HELP Knopf.
Trigonale Koordinaten in
der Form von 1,1,2 or 0,0,1 or 1,0,3 or 0,0,-1 ... -- >
um einen Kluster präzise zu platzieren. A) gewünschten Kluster aktivieren
durch anklicken und nochmals klicken. B) Textfeld anklicken und Koordinaten
in oben dargestellter Form von X,Y,Z (die Koordinaten gehen von 0 bis 9 und
können auch negativ gesetzt werden), C) den ALIGN Knopf klicken oder die
EINGABE Taste der Tastatur drücken, und dann D) den Mauskursor über
die Bildfläche bewegen. die Rotationsdrehwinkel können ebenfalls
eingegeben werden in der Form von
0,0,2,180,90,270, also als Xtrig,Ytrig,Ztrig,Xrot,Yrot,Zrot. Wenn nur Winkel
eingegegeben werden sollen ohne die position des ersten Würfels / Kugel zu
verändern, dann müssen die X,Y,Z Koordinaten leer aber Komma-getrennt
eingegeben werden: ,,,180,90,270 setzt Xrot auf 180, Yrot auf 90 und Zrot
auf 270
Grad ohne die Position des Klusters zu verändern (bitte beachten zwischen
den Kommas befinden sich KEINE LEERSCHLÄGE ! ).
Achtung der MS internet Explorer ist eigenartig und ermöglicht
Koordinateneingaben mit Komma getrennten Werten nur bei Bestätigung durch
Klicken von ALIGN und nicht durch Drücken der Eingabetaste.
Da es uns
ein Anliegen ist, dass der gesammte Kode in jeder html-Seite transparent
einsehbar ist, haben wir auf jegliche Verwendung von Includes verzichtet.
Möglichtst klassisches standart Java Script wurde verwendet im Zusammenspiel
mit der um 2015 eingeführten WEBGL Version von Open Graphic Language
(OpenGL). Die Puzzles laufen damit nur unter den seither eingeführten
Browsern. Ich habe den Kode getested auf Mozzila Firefox, Chrome, normal
und development Versionen, auf Opera und auf MS Explorer und Microsoft Edge
GLOSSARY Cluster_number <-> Cluster_names
1=cluster 2=clustname
1 PB_1F
2 PB_2F
3 PB_3F_180
4 PB_3F_60
5 PB_3F_120
6 PB_3F_90
7 PB_4F_180_180
8 PB_4F_180_60
9 PB_4F_180_120
10 PB_4F_180_90
11 PB_4F_120_120
12 PB_4F_60y120
13 PB_4F_120_240
14 PB_4F_90_90
15 PB_4F_90_270
16 PB_4F_120y240
17 PB_4F_90y180
18 PB_4T_60y60
19 PB_4T_60y120
20 PB_4T_60_90
21 PB_4T_90y120
22 PB_4R_120_120
23 PB_4R_240_240
24 PB_4R_120_240
25 PB_4R_240_120
26 PB_4R_90_120
27 PB_4R_270_240
28 PB_4R_90_240
29 PB_4R_270_120
30 PB_4R_60y90
31 PB_4R_300y270
32 PB_1Fa
33 PB_4T_60_60a
34 PB_4F_180_60b
35 PB_4F_180_60c
36 PB_4F_180_60c
37 PB_4F_180_60d