
|
|
PUBLICATION (n'existe qu'en englais) |
|
CES CASSE TÊTES ONT ÉTÉS DÉVELOPÉS EN CBT (COMPUTER BASED TRAINING)POUR AMÉLIORER L'IMAGINATION EN L'ESPACE TRIDIMENSIONEL.
Les casse têtes des poly cubes (PC) et poly boules (PB) ont été développé et introduit en 2015 au Musés Suisse du Jeu à la Tour de Peiltz (prés Vevey sur le Lac Léman en Suisse). Des prototypes en bois ont étés construits et montrés en accompagnant la présentation en forme de posters. Comme le cout de ces casse têtes dans cette forme serait prohibitive, nous avons mis en virtuel le tout en programmant en WEBGL (WEB Graphic Language), JAVASCRIPT et SVG (scalable vector graphiques). Ce choix de languages a l'aventage que ces languages de programmation en script (traitement en ligne par ligne sans nécessité d'assemblage du code) sont très courant et s'interprètent dans tous les exploreurs modernes version développeur de d'internet. Ce qui rend ces casse têtes indépendant des plateformes et se jouent sur la plupart des ordinateurs et téléphones mobiles. Nous avons développé le code sur la version développeur de MOZILA FIREFOX et l'ont testé sur les exploreurs Chrome, Opéra et MS Internet-Explorer et MS Edge. Aucune APP n'est donc nécessaire. En plus le code peut être lis et étudié par n'importe quelle éditeur de texte comme par exemple le Microsoft Notepad en mode de UTF-8. Bien sur on peut aussi inspecter le code sur la plupart des exploreurs (cliquer avec le bouton droite de la souris et choisir inspecter le code). Personnellement j'utilise toujours MS-FRONTPAGE pour programmer en combinaison le FIREFOX pour développeurs avec la console WEB pour la recherche des fautes. Nous avons expressément renoncé de l'utilisation de programmation de type "include", pour augmenter la lisibilité et la transparence en faveur des étudiants. Des commentaires sporadiques ont été faites comme aide pour développeur le code et point pour enseigner la programmation.
Notre travail est aussi en exemple pratique de démonstration du contenu du livre exceptionnel en anglais: WebGL Programming Guide, de K. Matsuda et R. Lea, 2015, Adison-Wesley, ISBN 978-0-321-90292-4. Les casse têtes présentes ici peuvent être vus comme un enseignement sur base d'ordinateur (CBT = Computer Based Training) pour apprendre à visualiser l'espace en trois dimensions et imaginer l'interaction d'objets tri dimensionnels, une compétence de grande importance pour les sciences naturelles, les techniciens et engenieurs, les architectes et ne pas en dernier lieu pour les auteurs de jeux en trois dimensions. En chimiste physicien je connais personnellement l'importance de pouvoir imaginer et visualiser des objets dans l'espace en 3 dimensions.
Deux types de casse têtes sont traités ici: les poly cubes et les poly boules. Des objets géométriques plus grandes comme des cubes, tétraèdres ou octaèdres sont assemblés à partir d'une multitude de polymères plus petites comme défini dans la publication précité. Les casse têtes en forme de cubes sont assemblés à partir de monomères a pentamères de poly cubes ou poly boules, et ceux des tétraèdres (pyramides à trois pentes) ou octaèdres sont constitués à partir de monomères au tétramères de poly boules. Par les définitions de la publication on obtient des cubes de 2 à 6 petits cubes par coté ou des tétraèdres de 2 à 8 boules par coté. Les casse têtes en forme de octaèdres sont définis ici même. La base cristallographique et donc les détails de la programmation sont bien plus simple pour les poly cubes et donc traité en premier lieu. La raison est le fait que dans ce cas tous deux les coordonnés de l'écran de l'ordinateur et les coordonnés du système basé dans l'objet (les polymères) sont orthogonaux. Le système de coordonnées à main droite consiste pour l'écran de l'ordinateur de l'axe X qui augmente de gauche vers la droite, de l'axe Y qui augmente du bas vers le haut et de l'axe Z qui augmente de l'écran vers l'observateur.
Les poly cubes 2x2x2 sont trés simple à assembler mais sont trés utliles pour se familiariser avec la surface d'utilisateur et les translations (déplacements des objets en direction des axes X, Y et Z de la vue) et rotations (tourner les objets autour leurs axes X, Y et Z basés dans les objets) des clusters (polymers). Ces exercises permettent aussi de comprendre la difference entre une solution d'un de ces casse têtes construits en bois, par exemple un cube fait à partir de poly cubes en bois, et son equivalent virtualisé sur un ordinateur. Si par exemple on tourne le cube assemblé en bois par 90 degrées on se rend compte qu'il s'agit toujours de la même solution. Dans le cas de la solution virtualisé sur ordinateur on se rend compte que de par la rotation de 90 degrées tous les coordinées et les angles de rotations des polymers concernés sont modifiés et donc le file JASON (Java Script Object Notation - voire aussi Store et Texte) qui contient tous les paramètres qui déterminent les placements de tous les objets. De même les 3x3x3 poly cubes sont simples à assembler y inclus le fameux Soma cube comme défini de Piet Hein. Les poly cube de taille superieur sobnt plus difficiles à assembler et surtout le 5x5x5 poly cube, qui pourait bien être un des puzzles les plus difficiles jamais découvert. En effet trouver une seule solution pour le 5x5x5 poly cube puzzle m'a bien couté deux mois de travail et cela avec un model en bois (ce qui est plus rapide pour chercher des solutions) et en plus avant de colorer les pièces en noir et blanc. Le 6x6x6 cube est plus simple a ssembler car il contient ausse le monomer, dimer et les trimers qui aident a combler les trous qui restent.
Exercisses avec des poly cube assemblages et constat de la multiplication des solutions dans le cadre de la virtualisation sur l'ordinateur.
Les exercisses avec le poly cubes seront traité d'abbord car on reste ici dans le cadre de systèmesde coordonnés orthogonaux, une simplification importante en comparaison avec les poly spheres. Les buts de ces exercisses est la familiarisation avec la surface de l'utilisateur, les translations (mouvements en direction X, Y ert Z de la vue) et rotation (tourner autour des axes X, Y et Z des polymers) des clusters, la rotation de la vue (en pas de 45 degrées autour l'axe Y du monde) le pivotement (Tilt, autour les axes du monde X / Y) de la vue (monde), le sauvetage locale de solutions pour permettre le progrés en trouvant des solutions, la découverte comment des solutions sauvés peuvent être recherché et comment une solution finale peut être présenté en diagram en deux dimensions (MAP). Divers assemblages de clusters qui permettent de construire des cubes 2x2x2 ou 3x3x3 ont été préparés pour permettre de se famliariser avec des clusters de complexité grandisant passant du monomer, au dimer aux trimers, aux polymers linéaires, aux polydmers plates (PC_1F, PC_2F, PC_3F, PC_4F, PC_5F et PB_1F, PB_2F, PB_3F, PB_4F), aux polymers tridimensiauneaux avec au moins une plane de mirroir (PC_4T, PC_5T et PB_4T), et finalement aux clusters qui existent en pairs racemiques (PC_4R, PC_5R et PB_4R) qui forment des images de miroirs mutuelles (comme nos deux mains qui forment aussi un pair racémique). La nomenclature des poly cubes (PC) et poly boulles (PB) sont indiqués en paranthèses. Ces exercises sont surtout censés de familiariser l'étudiant avec le mouvement et l'interaction des clusters.
Les poly cubes se constuisent couche par couche en direction de l'observateur, la couche la plus basse ayant été placé dans la plaine XY du moniteur. Une solution complète puet être présenté en forme de diagram 2D en cliquant le bouton Align, puis en écrivant MAP dans le champs de texte (appelé File) et finalement cliquant sur le champs de l'image (en alternative on peut commencer par ecrivant PLAN dans le champs de textee, au lieu de cliquer Align). Les couches sont montré sur le diagram en 2D en commencant par la couche posé le plus haut, qui se trouve le plus prés de l'observateur, cela dans le sense qu'on regarde la soultion du puzzle du haut vers le bas. C'est donc dans le même sense qu'on voit la solution en 3D pour le cas que la vision n'est pas tourné ou pivoté. On peut en effet pivoter l'objet du cube assemblé vers le bas et vers le haut en cliquant Tilt à répétition. L'assemblé de la solution peut aussi être tourné autour l'axe Y du moniteur (rotation du monde) en pas de -90, -45, +45, ou 90 dégrées. Le premier cube du premier cluster est toujours coloré en rouge pour aider à l'orientation. Aussitôt qu'un cluster est activé pour une translation ou rotation en le cliquant il est recoloré en vert: la première unité en vert intensive, la deuxième en vert-bleu, et les restants en vert pâle. Cette coloration aide à voir l'orientation du cluster dans l'espace 3D et pour pouvoir reconnaitre la direction des trois axes X, Y, et Z du système de coordonnées orthogonaux basés dans l'objet (les axes Zrot, Yrot et Zrot de rotation de l'espace modèle). Avec les poly cubes tous les angles de rotation autour Zrot, Yrot et Zrot sont limité à des incréments de 90 dégrées, et donc sur plus, moins 90 , 180 ou 270 dégrées.
Les poly cubes qui suivent ont étés construits pour le tutorial pour pouvoir se familiariser avec le comportement dans l'espace tri dimensionnel des clusters de formes complexes. Tous les clusters possibles jusque au pentamères sont illustrés schématiquement dans l'aide (HELP).
Commençons avec le poly cube 2x2x2. D'abord une remarque sur la nomenclature: PC indique qu'il s'agit d'un poly cube et PC_2x2x2 que la solution finale de cet assemblage représente un cube de deux sur deux sur deux unités par axe de modèle X, Y et Z; " cl_ " suivi d'un nombre (ou plusieurs nombres séparés par _) identifie les clusters qui font partie de l'assemblage, comme énuméré et définie dans le compendium du HELP (voir ici-bas). WEBGL_PC_2x2x2_cl1_2_2_4 par exemple contient le monomère 1, deux fois le dimer le 2 et 2bis et le trimmer 4 en forme d'angle droite. Ouvrez cet exemple et essayez de résoudre ce casse tête extrêmement simple en construisant un poly cube 2x2x2. Une fois fini et ayant contrôlé la solution en tournant et pivotant l'assemblage vous cliquez Align et ensuite écrivez MAP dans le champs de texte pour voir le diagramme en 2D de votre solution. Il est important de reconnaître la différence entre une solution d'un modèle en bois et d'une solution virtuelle dans un ordinateur: les positions de chaque cluster, exprimé en coordonnées X,Y et Z du premier cube du cluster, et des trois angles de rotation Zrot, Yrot et Zrot autour des trois axes de rotation du système des coordonnés du modèle caractérisent chaque cluster dans une solution comme exprimé par une matrice de solution. Des differences dans ces assemblages de donnés exprimés par ces matrices de solution peuvent donc faire croire qu'il s'agit de différentes solutions pour une et la même solution physique. Prenez en exemple les assemblages qui suivent, pour lesquelles il n'existe à chaque fois qu'une seule solution physique: WEBGL_PC_2x2x2f_cl26, WEBGL_PC_2x2x2c_cl10, WEBGL_PC_2x2x2d_cl11, et WEBGL_PC_2x2x2e_cl12. Chacune de ces solutions d'un cube de 2x2x2 peut en effet être placé de 24 manières sur une surface: chaque cube peut être placé sur une des ces 6 surfaces, bas, haut, gauche, droite, devant, derrière, et une fois placé de tel sorte chaque cube peut encore être tourné pr 0, 90, 180, et 270 dégrées autour de l'axe Z de l'assemblage. Cela montre clairement la différence importante de fond entre un modèle en bois et une solution virtuelle dans un ordinateur: chaque placement de l'assemblage finale constitue une autre solution pour l'ordinateur avec une pile de matrice de l'objet modèle différente (Object Model Matrix Stack) comme exprimé en JASON (JAva Script Object Notation) par un document de texte différente.
Pour approfondir tout cela ouvrez WEBGL_PC_2x2x2f_cl26 par un click de la touche droite du souris et ouvrez dans un nouvel registre du browser. Le scrolleur à droit du bouton Block montre le chiffre 1 en ouvrant pour la première fois. En changeant le choix vers S=Sol. et ensuite bougeant le cursor à travers le canvas (la toile de l'image) vouz voyez que les trois clusters, le monomer, le dimer et le cluster numero 26 = PC_5T_90_0_90, sautent dans la seule solution physiquement possible. En cliquant sur Align, écrire MAP dans le champs de texte et cliquer sur la toile, apparait le diagram en 2D de la solution suivi par un texte qui présente le contenu de la pile de matrice de l'objet modèle de la solution en nomenclature JASON. Chaque cluster est présenté en affichant chacun de ses cubes avec leurs coordonnés dans l'espace modèle X,Y et Z et les rotations Zrot, Yrot, Xrot comme défini pour le premier cube du cluster. Le diagramme montre graphiquement chaque cube avec son coloris, le numéro de son cluster, et sa séquence dans cette cluster (et b pour black et w pour white) comme il apparait vu d'en haut vers le bas, couche par couche, comme indiqué plus haut. Le texte JASON montre la même chose mais en séquence du pile de la matrice de l'objet modèle. En cliquant sur le scroller on trouve les 24 positionnements de cette unique solution physique dans l'espace virtuelle de l'ordinateur, préprogrammé sur la page html, avec les surfaces de positionnement indiqués en anglais (front = avant, back = devant, bottom = en dessous, top = en dessus, left = gauche, right = droite) et les angles de 90, 180, 270 dégrées de rotation au sens de la montre vu d'en bas de l'axe Z du moniteur (dans le sens positive du système des coordonnées de main droite). En cliquant deux fois sur le cluster 29 vous pouvez le colorier en vert. En maintenant changeant le positionnement en choisissant entre les différent solutions virtuelles, tous les trois clusters restent identifié parleusr coloris: rouge le monomère, blanc et noir le dimer et vert le pentamère. Comme ça vous pouvez étudier les différentes positionnements en pivotant et tournant l'assemblage (le coloris reste autant que vous ne cliquez pas sur la toile). Un commentaire concernant le texte JASON; Align / MAP ne fonctionnent que pour les solutions finis. Part contre on peut sauver tous les états d'une solution en développement dans l'explorer locale en cliquant Store. En cliquant Text après cela on peut imprimer la pile de la matrice de l'objet, cette fois seul une parenthèse [] par cluster apparait (contrairement à Align / MAP ou chaque cube de chaque cluster donne une parenthèse JASON).
Il est amusant de constater, que les choses deviennent encore bien plus complexes pour le "casse-tête" WEBGL_PC_2x2x2a_cl8 le plus simple qu'on puisse imaginer, qui réunit deux fois le tertramer cyclic et plate, numero 8. Quand on regarde un modèle en bois on trouve qu'une seule solution valable, toute en remarquant qu'il existe aussi une mauvaise solution qui place les noirs côte à côe (et aussi les blancs côte à côte). Ovrant le file et regardant le contenu du scroller (voir tout en bas du scroller) on constate qu'on peut en effet definir 8 solutions dans l'ordinateur (voir le texte en anglais pour l'explication). Chacune des 8 solutions peut être placé de 234 façons et donc on arrive à 96 solutions dans l'espace virtuelle de l'ordinateur pour une seule solution physique. Ce fait est à considerer quant on interprète les resultats de simulations de solutions par ordinateur!
Le tetramer tridimensional qui contient une plaine de symmetrie (WEBGL_PC_2x2x2c_cl10), la paire racemique des tetraedres ( WEBGL_PC_2x2x2d_cl11 et WEBGL_PC_2x2x2e_cl12 ) et selement deux de tous les pentamères, c'est à dire les numeros 25 et 26 ( WEBGL_PC_2x2x2f_cl26 ), peuvent servir à construire des poly cubes 2x2x2. Le puzzle WEBGL_PC_2x2x2b_cl4_11 est un cas appart comme un des deux clusters 11 se construits a part du monomrer et du trimer à angle droite, ce qui provoque une solution virtuelle suplémentaire. Deux clusters 10 se complémentent pour former un cube 2x2x2, tout en constatant que un des deux clusters 10 doit être récoloré pour empêcher de finir avec une fausse solution (noir à côté noir). La paire racemique des clusters 11 et 12 ne s'assemblent pas pour former un cube 2x2x2. Par contre deux fois les mêmes clusters du paire WEBGL_PC_2x2x2d_cl11 et WEBGL_PC_2x2x2e_cl12 forment des solutions en 2x2x2 cubes dont les solutions eux mêmes forment de nouveau une paire racémique, comme ces solutions sont des images de miroir mutuelles.
Plusieurs 3x3x3 poly cube puzzles ont été faits pour pouvoir faire la connaissance des autres pentamères tri dimensionnels, cela en combinaison aves les clusters plats qui n'ont que peux d'éléments de symétrie internes. Le fameuse cube Soma, introduit par Piet Hein, est de cette classe. Les divers puzzles de poly cubes 3x3x3 sont de très bons candidats pour apprendre l'approche a trouver des solutions à des puzzles en 3D dans l'espace virtuelle. Il est bien sur nécessaire de pouvoir sauver les progrès en cherchant une solution. Pour cela nous avons préparé deux façons de sauvetage coté client: le sauvetage spécifique au browser se servant du modèle DOM (Document Model Object) et sauvetage en faisant un document de texte. La première méthode est plus volatile en que le sauvetage se fait dans le browser même et donc li faut se servir du même browser sur le même ordinateur pour sauver et récupérer l'information. La migration d'un à l'autre ordinateur n'est donc pas possible. Le texte visible dans le champ de texte est utilisé dans ce cas comme nom de sauvetage, ce qui veut dire que des suites de progrès en trouvant une solution peuvent être sauvés. Les boutons Store (= sauver), Load (=charger) Text (= montrer JASON text) et Erase (= effacer la mémoire) et le champs pour entrer du texte après le mot File: sert à entrer les noms de sauvetage. Commençons un exercice en ouvrant WEBGL_PC_3x3x3 et cherchant S=Sol. dans le Scroller puis bouger le curseur à travers la toile pour faire sauter la solution sur l'écran. Cliquer le dernier cube en haut à droite et le tirer vers la droite et re-cliquer le cluster pour l'immobiliser et finalement cliquer Store. Maintenant recharger le browser ou alors choisir le ligne de séparation ----- dans le scroller, ce qui réinitialiser le puzzle. Si on clique maintenant le bouton Load on voit réapparaitre la solution défaite avec le cluster 6 tiré vers la droite comme on l'avait sauvé sous le mot vide (comme on n'avait pas donné un nom ci-dessus et le champ de texte était resté vide).
En démonstration de la deuxième méthode de sauvetage indépendant du browser utilisé, plus permanente et plus flexible, cliquez sur le bouton Texte et notez que l'information sauvé ci-haut, apparait maintenant en forme de queue continu de texte JASON, qui commence et termine avec des double parenthèses [[---JASON TEXTE---]] , que l'on copy / insére (avec Ctrl C / Ctrl V ) pour l'insérer dans un pure éditeur de texte ASCII, comme par exemple le Microsoft Notepad, pour sauver ce document sous n'importe quelle nom, par exemple SOLUTION, dans vos dossiers préférés. Maintenant recharger le browser ou alors choisir le ligne de séparation ----- dans le scroller, ce qui réinitialiser le puzzle. Maintenant cliquer sur le bouton Browse et chercher votre dossier et texte sauvé sous SOLUTION et cliquer ouvrir comme d'habitude et bouger le curseur à travers la toile. Pour commentaire importante: avant le sauvetage d'une solution il faut toujours cliquer Align affin de rassurer que tous le coordinées et surtout tous les angles de rotation sont arrondis et vérifiés pour être compatibles avec la forme cristalline rencontré dans le puzzle.
Pour en revenir sur la discussion de la différence entre les solutions et le positionnement de solutions du 2x2x2 poly cube WEBGL_PC_2x2x2a_cl8, j'ai trouvé sur internet des discussions sur le nombre de solutions du Soma cube de Piet Hein WEBGL_PC_3x3x3Soma le suivant: une des sources parle de 240 solutions pour le 3x3x3 Soma cube de Piet Hein (http://puzzler.sourceforge.net/docs/polycubes.html et http://puzzler.sourceforge.net/solutions/cubes/soma-3x3x3.txt ). D'autre part on trouve dans http://mathworld.wolfram.com/SomaCube.html le commentaire qui indique que 1'105'920 solutions sont à attendre basé sur les propriétés de symétrie. Dans le deuxième cas il doit avoir confusion entre solutions et positionnement. Nous avons préprogrammé seulement 2 solutions pour le Soma cube, mais en vue des 240 solutions il n'est pas un puzzle difficile a trouver une solution et en effet selon mon expérience on arrive en 15 à 30minutes à trouver une solution. Les 3x3x3 puzzles qui suivent ont été assemblée pour se familiariser avec la surface d'utilisateur et en même temps faire connaissance avec tous les clusters des poly cubes: WEBGL_PC_3x3x3, WEBGL_PC_3x3x3a_cl30_31_33_34, WEBGL_PC_3x3x3b_cl30_31_32_35, WEBGL_PC_3x3x3c_cl18_19_22_24, WEBGL_PC_3x3x3d_cl31_37_38_39, WEBGL_PC_3x3x3e_cl36_39_40_41, WEBGL_PC_3x3x3f_cl25_27_28_29_32, WEBGL_PC_3x3x3Soma. Pour ouvrir la débatte sur les casse têtes des poly cube, j'ai assemblé un cube de 4x4x4 à partir de tous les paires racémiques des pentamères, plus le dimer et le trimer linéaire WEBGL_PC_4x4x4a_racemics. Je serais étonné si une solution était possible: pour le cas que vous en avez trouvé une, contacté moi sur brordorf@gmail.com .
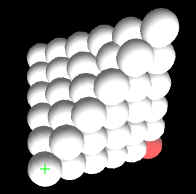
Cristaux de roche: Les mêmes clusters des poly cubes, cette fois construits à partir de sphères.
Les mêmes casse têtes d'en haut cette fois assemblés en poly boules cubes: WEBGL_PBC_2x2x2, WEBGL_PBC_2x2x2a, WEBGL_PBC_2x2x2b, WEBGL_PBC_3x3x3, WEBGL_PBC_4x4x4, WEBGL_PBC_5x5x5, WEBGL_PBC_6x6x6. La solution présent par exemple pour WEBGL_PBC_3x3x3 montre bien qu'il s'agit du cristal de roche du NaCl. Les atomes blancs alternent d'une façon régulière avec les noirs et ils s'agit d'une part des cations du sodium et d'autre des anions du chlore.
Définition des clusters et ordre de rotation des clusters autour les axes Zrot, Yrot, et Xrot du système de coordonnés du modèle.
Le contexte géométrique est bien plus complexe pour les casse têtes des poly boules que pour les poly cubes. Les puzzles présenté ici sont basés sur le réseau cristalline le plus dense cubique, dont les couches alternent en séquence abcabc... étant présenté dans un système de coordonnés trigonaux. Les angles entre les axes x,y, et z de ce système de coordonnées sont de 60 dégrées. Le diagramme qui suit montre l'arrangement des sphères en fonction des valeurs x,y, et z pour 3 couches superposés dans la direction de l'axe z. Les lignes solides présentent les sphères avec z=0 (couche a -> dans la plaine du moniteur), les lignes foncés tiennent pour z=1 (couche b -> en s'approchent du spectateur), et lies lignes cassés pour z=-1 (couche c -> en l'éloignant du spectateur). Avec les poly cubes le système orthogonal x,y,z des cubes reste en accord superposé avec le système orthogonal du moniteur X,Y et Z et donc tous les coordonnées entiers des poly cubes restent des chiffres entiers pour le système du moniteur. En plus tous les angles de rotations des clusters restent des multiples de 90 dégrées dans le deux systèmes. Pour le système trigonal, aucun des ces avantages tiennent debout et les coordonnées doivent être recalculés en permanence en faisant des aller-retour entre le système basé du modèle au système du moniteur. Concernant les angles de rotation on s'aperçoit en étudiant les détails, que le comportement dans le système trigonal est en effet excessivement complexe. En plus on s'aperçoit que les clusters faisant partie du système du réseau cristalline le plus dense cubique peuvent contenir des angles trigonaux (des multiples de 30 degrés) et cubiques ou orthogonaux (des multiples de 90 dégrées) en combinaison. Les pièces linéaires sont des membres des deux systèmes. Les clusters poly boules 6, 10, 14, 15, 17 sont des exemples cubiques pures. Les paires racémiques (des cluster tridimensionnelles qui ne contiennent pas de plane de miroir interne) 26 et 27, ou 28 et 29 sont des exemples de clusters qui contiennent un mélange d'angles trigonaux et orthogonaux. La table ci-dessous montre les facteurs de conversions entre le système orthogonale du moniteur X,Y, Z et les chiffres entiers du système trigonal nx, ny, nz. Ceux qui s'interessent à la programmation en JavaScript, peuvent étudier la fonction function Align_keydown(ev, gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) sur les lignes 2303 à 2348 ou ses facteurs de conversion sont utilisés dans le puzzle WEBGL_PB_4x4x4 , après avoir ouvert la source par cliquant la touche droite de la souris. Ces facteurs sont aussi utilisés dans la fonction function trigCoordinatesParser() sur les lignes 3658 à 3714 et on observe, que les puzzles des tétraèdres sont posés sur la plaine XY du moniteur en grandissant couche par couche en direction du Z vers l'observateur.
Tous les clusters des poly boules sont définis de même sorte avec la première boule centré sur 0,0,0 (x=0, y=0, z=0) et la deuxième boule toujours sur 1,0,0 (x=1, y=0, z=0). Ce système de définition induit à une importance particulière des coordonnés z, y, et y de la deuxième boulle, car cet elle qui donne l'orientation générale du cluster dans le réseau trigonale du système cristalline le plus dense cubique. Une fois placé de cette manière n'importe quelle cluster peut être placé d'une façon définitive dans le réseau trigonale du système cristalline le plus dense cubique par une seule rotation autour de l'axe Xrot du système de coordonnés basé dans objet du modèle. Donc en changeant la séquence de rotation de Xrot, Yrot, Zrot vers Zrot, Yrot, Xrot, tout en recommençant l'opération de tous ces rotations à chaque fois du début, on constate que la rotation Xrot n'est plus dépendant (couplé) aux rotations Zrot et Yrot. En autre mots ne pas suivant ce système de définitions et de séquence de rotations on remarque que Xrot et Yrot, et aussi Yrot et Zrot, sont couplés, ce qui veut dire que Yrot et Zrot devraient être recorrigés après avoir tourné par Xrot (ce qui amènerai le fameux Gyrolock et nécessiterai une transformation vers l'espace complexe en utilisant les quarterions). Il faut se rappeler de ce mécanisme de rotations en permanence en cherchant des solutions à ces puzzles et toujours commencer en plaçant d'abord les deux premières boules (la boule en vert intense et la boule en vert-bleu) correctement dans le réseau cristalline en tournant d'abord autour Zrot (c'est à dire dans la plaine X-Y du moniteur), puis autour Yrot (axe, qui s'est bien sur modifié avec l'objet en tournant autour Zrot). Seul après un positionnement précise en cliquant Align il faut procéder en plaçant le cluster complètement dans le réseau cristalline en tournant autour Xrot. Finir par cliquant une deuxième fois Align et après cliquer Store.
Le diagramme qui suit montre le réseau cristalline le plus dense cubique avec tous les angles trigonaux et cubiques possibles pour la rotation dans la plaine x-y du moniteur (rotation autour les axes Zrot et Yrot). Les angles de 60 dégrées, par exemple, existent en plaçant la deuxième boule sur le plaines de z=+1 ou z=-1. Ces angles peuvent être modifié ensuite par 54.74 dégrées, l'angle entre le bords et plaines voisines, ou par 70.53 de, l'angle entre plaine et plaine voisine. Ces angles modifiées jouent surtout une rôle importante pour les rotations autour Xrot pour accommoder les clusters dans le réseau cristalline le plus dense cubique. Pour trouver toutes le angles possible par expérimentation, les solutions des puzzles des pyramides de boules de 3x3x3, 4x4x4 et 5x5x5 ont étés modifié d'une façon systématiques en pivotant et tournant les solutions en créant des nouveaux placements. Les angles dominantes trouvé sont mis en rouge dans la table qui suit. Le placement exacte est primordial pour la réussite d'une solution dans le cadre du réseau cristalline le plus dense cubique et un mécanisme à donc été développé pour placer tous les clusters avec des coordonnées et angles précisément définis, mécanisme déclenché en cliquant Align. C'est seulement aprés avoir placé les premières boules précisément dans le réseau cristalline, qu'on procède de finir le placement en tournant autour l'axe Xrot en cliquant le bouton z>x qui se transforme en z>x par cette mesure. Si un angle de rotation est loin d'une valeur permis en cliquant Align on obtient un message d'erreur dans la forme de "1 Bad trigonal orientation dX=0.5 dY=0 dZ=1 of clust_5" (1 mauvaise orientation trigonale dX=0.5 dY=0 dZ=1 du cluster 5). Les essais sont contés de 1 à 3 (le chiffre 1 avant Bad) et c'est après le troisième essaie sans succès que chacun des trois angles seront remis à 0 dégrées. Remarquez le dX = 0.5 qui indique le problème du placement de la deuxième boule entre deux couches!
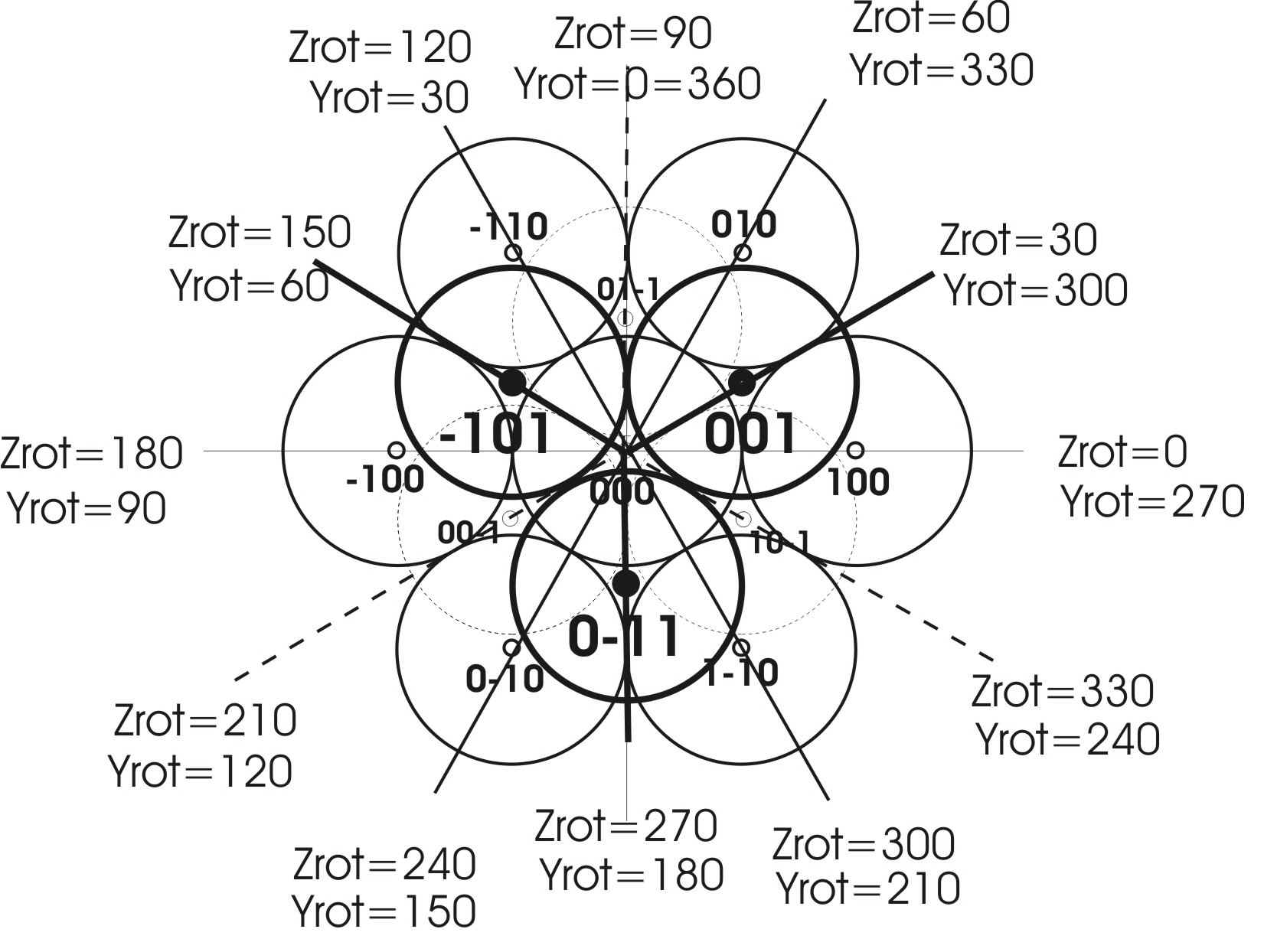
| Angles trigonales possibles | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Angles orthogonales possibles | 90 | 180 | ||||||
| Tous les angles possibles | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Angle arête-surface = | 54.74 | plus | 84.74 | 114.7 | 144.7 | 174.7 | 204.7 | 234.7 |
| 360 | minus | 335.3 | 5.26 | 35.26 | 65.26 | 95.26 | 125.3 | |
| Angle surface-surface = | 70.53 | plus | 100.5 | 130.5 | 160.5 | 190.5 | 220.5 | 250.5 |
| neg + | 360 | minus | 319.5 | 349.5 | 19.47 | 49.47 | 79.47 | 109.5 |
| Tous les angles possibles | 210 | 240 | 270 | 300 | 330 | 360 | ||
| Angle arête-surface = | 54.74 | plus | 264.7 | 294.7 | 324.7 | 354.7 | 384.7 | 54.74 |
| minus | 155.3 | 185.3 | 215.3 | 245.3 | 275.3 | 305.3 | ||
| Angle surface-surface = | 70.53 | plus | 280.5 | 310.5 | 340.5 | 370.5 | 400.5 | 430.5 |
| minus | 139.5 | 169.5 | 199.5 | 229.5 | 259.5 | 289.5 |
Des essais avec des assemblages de poly boules pour se familiariser avec le réseau cristalline le plus dense cubique.
Ouvrez le plus simple des puzzles poly boules, le WEBGL_PB_2x2x2 êt tachez de construire une pyramide de boules à deux boules par coté en tirant pour commencer le deuxième dimer vers la gauche. Placez la boule verte en dessus la boule rouge et la boule blanche en formant un triangle et cliquez Align. Ensuite vous cliquez le bouton Rot (Rotate) et placez ensuite la boule vert-bleu en dessus du triangle rouge-blanc-vert (c'est à dire en la tirant vers vous, l'observateur du moniteur). Recliquez Align et observez comme la boule vert-bleu saute dans la position requise en formant un tétraèdre, en cas que vous avez bien placé la boule vert-bleu au bon endroit en direction positive de l'axe z du système orthogonale du moniteur. Si par contre vous avez placé la quatrième boule dans la mauvaise direction, c'est à dire en sens négative de l'axe Z, vous recevez un message d'erreur de la forme de "1 Bad trigonal orientation dX=-1 dY=1 dZ=1 of Clust._48". Ce qui indique que cette position dans la mauvaise direction n'est pas compatible avec le réseau cristalline le plus dense cubique. Un regard sur le diagramme ci-dessus donne l'explication. L'axe trigonale x est congruent avec l'axe x trigonale du moniteur qui grandit de gauche vers la droite en pointant de la boule 0,0,0 vers la boule 1,0,0 . L'axe trigonale y par contre n'est pas congruent avec l'axe y du moniteur. Bien qu'elle est toujours couché dans la plaine x-y du moniteur, l'axe trigonale y pointe avec un angle de 60 dégrées et non 90 dégrées (entre x et y) de la boule 0,0,0 vers la boule 0,1,0. La troisième axe trigonale, finalement, pointe vers l'observateur, mais bien avec des angles de 60 dégrées vis-à-vis les axes trigonaux x et y, ou avec un angle de 54.74 dégrées par rapport à la plaine du moniteur qui contient la base de la pyramide. La direction juste pointe donc de la boule 0,1,0 vers la boule 0,0,1 ce qui par déplacement parallèle vient au même que 0,0,0 vers 0,-1,1. Cette complication est une conséquence de la suite des couches abcabc... dans le réseau cristalline le plus dense cubique. En résumé la pyramide est placé en dessus de plaine du moniteur en direction de l'observateur. La pyramide de 2x2x2 boules peut bien sur aussi être construit en plaçant le premier cluster avec la boule rouge en direction du boule rouge à 0,0,0 vers 0,0,1 (et chaque dimer peut bien sur aussi être renversé en direction). Une analyze détailée de toutes positions trigonales possible à été documenté dans WEBGL_PB_3x3x3TrigonalAngleAnalysis .
Dans l'exercice par le puzzle WEBGL_PB_3x3x3 on construits une pyramide de boules à partir de trois clusters en forme de trimères non-cycliques et cela peut démontrer comment il faut placement un cluster poly boules trigonal (cluster_5 = PB_3F_120) en comparaison d'un cluster poly boules cubique (cluster_6 = PB_3F_90) dans le tétraèdre de boules. Dans la suite une instruction pas par pas comment reconstruire une des solutions présent dans le scroller. D'abord déplacer la boule rouge vers la gauche et ensuite tirer le trimer linéaire vers la gauche en plaçant la boule en vert intense sur le point 0,0,0, puis cliquer Align. En prochain déplacer le trimer à angle droite (cluster_3) en plaçant la première boule au dessus la première boule du cluster 6 en direction de l'axe y trigonale, ce qui place sa deuxième boule vert-bleue en dessus de la deuxième et troisième boule du cluster 3, et Align. Ensuite cliquer Rot (ou Rotate) et comme les premières deux boules du cluster sont correctement placé dans le réseau cristalline cliquer le bouton z>x pour pouvoir tourner le cluster autour Xrot. Pour cela cliquer le cluster 6 et tirer le curseur du souris en ligne droite vers le haut en direction de l'axe y du moniteur pour tourner le cluster en sens positive autour Xrot. Pour plus de contrôle on aurait aussi pu cliquer le glisseur x et tenir la touche droite de curseur (>) jusque à ce que la troisième boule soit bien placé, pois cliquer Align. Alors cliquer Trs (ou Translate) pour déplacer le cluster trigonale (cluster_5) en plaçant sa première boule en dessus (direction y du moniteur) des deux premières boules du cluster 6 (le bouton de la mode du translate montre x>z). Après avoir cliqué Align on constate que tous les trois premières boules des clusters 3,6 et 6 sont posé sur l'axe y trigonale, donc avec les coordinés 0,0,0 , 0,1,0 et 0,2,0 (x=0', y=2, z=0).
Maintenant il faut déplacer la deuxième boule du cluster 5 par un mouvement de rotations vers la position 0,1,1 , c'est à dire elle doit être posé en dessus de la première et deuxième boule du cluster 6 (en dessus = en direction positive des l'axes z du moniteur et du système trigonale). Pour achever cela cliquer Rot (ou Rotate) et laisser sur z>x (oder Z->X) pour permettre des rotations autour Zrot et Yrot pour placer la deuxième boule avec le souris, puis cliquer le cluster. Alternativement pour utiliser les glisseurs, d'abord cliquer le cluster ce qui libère le curseur du cluster et permet de cliquer sur le glisseur Z, puis tenir la touche droit de curseur ( > ) en bas pour tourner la boule vert-bleu par 90 (ou 270) degrées autour de Zrot pour placer la boule vert-bleu exactement en dessus (en dessous) dans le sens du y du moniteur. Ensuite cliquer le glisseur Y et tenir le curseur droite (>) pour placer la deuxi>ème boule du cluster 5 en dessus (en direction z) des boules qui suivent: première boule du cluster 6 et deuxième boule du cluster 3, puis cliquer Align. Après avoir cliqué le glisseur X on peut placer la troisième boule. On peut aussi placer la troisième boule avec le souris après avoir cliqué z>x (ou Z->X ). D'abord cliquer Align et puis en répétition +45 pour pouvoir voir la pyramide en croissance de tous les cotés. Pour finir il faut encore placer la boule solitaire rouge en haut sur la pyramide. Pour cela cliquer Trs (ou Translate) pour retourner de la toile bleu la toile noire. Si on déplace la boule rouge vers la droite, elle disparait sous la pyramide. Pour la déplacer vers le haut de la pyramide il faut d'abord cliquer x>z (ou X->Z). Au lieu de cliquer x>z, on aurait aussi pu tourner la vu du monde par 90 dégrées (deux fois cliquer +45). La troisième méthode la plus élégante consiste à entrer les coordonnées 0,0,2 dans le champ de texte après avoir activé le cluster et pour finir cliquer Align. Notez qu'une deuxième solution à été préprogrammé dans le scroller du puzzle WEBGL_PB_3x3x3 et qu'un changeant d'une à l'autre solution la boule sur 1,0,1 se déplace légèrement. Cela est une conséquence des erreurs d'arrondissement pour le cluster cubique (cluster_6 = PB_3F_90).
Pour démonstration des placements possibles des clusters cubiques dans la pyramide tétraédrique on a produit les assemblages qui suivent. L'exemple WEBGL_PB_3x3x3a_cl7_cl10.html ne montre qu'un fragment de pyramide, et l'intérêt de WEBGL_PB_3x3x3b_cl26_cl27 et WEBGL_PB_3x3x3c_cl30_cl31 consiste au fait que tous deux contiennent des paires de clusters racémiques qui en plus contiennent des angles cubiques (90 ou 270 degrées) et trigoneaux (60 ou 120 degrés). Comme étude chercher les solutions dans le scroller. Puis clique Align et écrire MAP dans le champs de texte et cliquer sur la toile, à ce qu'apparaisse la solution en 2D sous la toile (toile = canvas). Ensuite prenez une prise de l'écran de la solution (pour un logiciel screen shot suivez http:hyperionics.com), puis choisissez ----- et reconstruisez la solution d'après le plan 2D.
Tous les puzzles de pyramides tétraédriques de poly boules 4x4x4 et 5x5x5 contenu ci-haut ont été utilisées pour déterminer avec précision tous les angles Xrot, Yrot et Zrot qui peuvent exister dans le système de coordonnés orthogonale basé dans le modèle pour le réseau cristalline le plus dense cubique. Comme pour les puzzles des poly cubes, cela était fite en flippant et tournant les solutions en tous les placements possibles. Un regard dans les scroller des tétraèdres des poly boules montre que bien sur il y a moins de placements possibles que avec les poly cubes ce qui simplifie aussi la nomenclature. S signifie la solution, R est utilisé pour pivoter vers la droite (R = flipp on Right side surface), L vers la gauche (L = flipp on Left side surface), F pour pivoter vers l'avant (F = flipp on Front surface). Cela est combiné avec des rotations du tout par des angles en pas de 60 dégrées dans le sens de la montre, donnant S60cw, R60cw, L60cw, F60cw (cw = clock wise), ou contre la montre, donnant S60ccw, R60ccw, L60cw, F60ccw (ccw = counter clock wise -toujours d'après le standard du système de la main droite de Zrot). Il s'agit seule de rotations "externes" du tétraèdre, donc ne pas des rotations "internes" possibles pour certains clusters comme par exemple les clusters 4, 14, 18, qui sont de toute façon déjà traités par les rotations et pivotements précédents! L'analyse complète peut être téléchargé pour plus de transparence et pour étudier la multitude de configurations sauvées dans WEBGL_PB_3x3x3TrigonalAngleAnalysis :
Télécharger WEBGL_PB_AnglesAnalysis in EXCEL for Windows: WEBGL_PB_AnglesAnalysis.xls
Le 3x3x3 tétraèdre, d'une grande simplicité, a
été spécialement conçu pour l'analyse des angles de rotation en contenant une
seule boule, un trimer linéaire et les deux trimères non-linéaires les plus
simples. Les derniers contiennent soit un angle trigonale de 120 degrés, ou un
angle orthogonal de 90 degrés. L'avantage du monomère est son indifférence aux
rotations, donc le fait que son état est simplement défini par ces coordonnées
x, y et z. Le trimère linéaire est de même indifférent aux rotations autour son
axe x. En comparaison du dimer, le trimère linéaire a l'avantage, que les angles
des rotations autour ses axes y et z, peuvent être déterminés avec le double de
précision. Le cluster trigonale se place dans une des plaines trigonales qui
sont placées parallèles aux surfaces du tétraèdre et qui ont des symétries de 6
temps de rotation en plaine. Le cluster non-linéaire orthogonal, par contre se
place dans une des plaines cubiques, qui sont placés d'une façon parallèle à
deux des arêtes non intersectées du tétraèdre. Ces plaines ont des symétries de
rotation en plaine de quatre temps. Deux boules supplémentaires ont étés
introduites comme témoins des positions des dernières boules de clusters. Ce qui
permet de trouver les angles de rotation d'une façon expérimentale en
réorientant un cluster mal placé après une rotation de l'ensemble, c'est à dire
d'une solution du tétraèdre. La raison pourquoi nos avons préférés cette méthode
plus élaboré aux quaternions, est pour pouvoir travailler avec des angles réales
dans la pile de la matrice modèle au lieu des angles imaginaires associés avec
l’approche quaternion. Remarquez que tous les résultats de cette étude sont
contenus dans le codage de la fonction function Angle_combinations(i, il, Xrot,
Yrot, Zrot, Xrot_ini, Yrot_ini, Zrot_ini, Rx, Ry, Rz). Cette fonction a été
introduite pour pouvoir tourner les assemblages de clusters dénommés block. Le
nom du block dénommé 1, a été réservé pour le block formé par tous les clusters
définis dans une certaine page html chargé dans l’exploreur et généré en
écrivant LOCK dans le champ de texte pour nommer des files.
Le mécanisme dite LOCK, permets de serrer tous les clusters (grappes = unités du
puzzle) contenu dans l’assemblage d’une solution trouvé dans le bloc commun
dénommée 1, affin de pouvoir tourner la solution dans une nouvelle position du
tétraèdre. Une telle rotation est une transformation complexe par le fait qu’il
y a interaction entre les systèmes de coordonnés orthogonaux du moniteur de
l’ordinateur, du monde de présentation du puzzle en 3D, et le système trigonal
de la pyramide à tétraèdre. Tourner autour de l’axe z est simple avec des
intervalles de 120 dégrées résultant en nouveaux positions trigonales qui
permettent d’activer la fonction de alignement. Echanger la surface de base de
la pyramide tétraédrique peut se faire en pivotant la pyramide par 109 degrés
autour l’axe x, suivi par une rotation autour l’axe z. Autrement un échange peut
se faire en pivotant par 109 ou 251 degrés autour l’axe y. Dans ce cas il y aura
une séquence de rotation autour z, autour y et enfin de nouveau autour z à
faire. Il faut sauver et recharger les états intermédiaires, par contre ces
états de transition ne peuvent pas être alignés, car il ne s’agit pas de
positions régulières du tétraèdre. Pour sauvegarder il faudrait d’abord
desserrer le bloc en écrivant UNLOCK dans le champ de texte. Aussi est il
judicieux de transformer un assemblage pour pousser la premier boule en bas vue
de gauche sur les coordonnés 0,0,0 indiqué par la croix verte sur le « canvas ».
Sinon il se peut qu’une solution correcte peut se défaire en désordre en
cliquant Align. Ce qui indique que les premières boules des clusters concernés
se trouvaient à mi-chemin entre deux positions intégrales.
Voilà une instruction de pas à pas pour renverser un tétraèdre vers
l’observateur autour l’axe x du moniteur : Alignez la solution choisi en
cliquant Align, écrivez LOCK dans le champs de texte, choisissez n’importe quel
cluster, changez vers Rotate, cliquez Block, cliquez le ajusteur X et le
déplacez avec le clavier ► pour arriver à l’angle 109 comme indiqué dans le
champ de texte de File. Cliquez Block, cliquez la surface bleue du canvas 3 fois
pour ne choisir aucun cluster, cliquez Erase, et puis Store. Cliquez le bouton
refresh ( ﺡ ) de l’exploreur et le bouton Load, remettez sur Rotate, choisissez
un cluster (ne cliquez pas Align comme la solution du tétraèdre ne se trouve pas
dans une position régulier du tétraèdre), cliquez Block, le glisseur Z et bougez
avec ► pour arriver à 60 degrés, puis cliquez Block et finalement Align. Voilà
on vient de reposer la solution sur l’ancien surface en face de l’observateur.
La solution est restez la même, mais pas pour l’ordinateur, comme la pile de la
matrice modèle a complètement changé, ce qu’on peut constater en cliquant le
bouton Text après avoir sauve l’état en cliquant Save.
Dans un deuxième exemple nous changeons la surface de base en tournant autour
l’axe y : chargez par exemple la solution S5 dans le sélecteur de solutions,
écrivez LOCK dans le champs de texte, changez à Rotate, cliquez Align,
choisissez un cluster, cliquez Block pour bouger le tétraèdre, déplacez le
glisseur Z pour 330 degrés, cliquez Block, Erase, Store. Cliquez le bouton
refresh ( ﺡ ) de l’exploreur et Load, écrivez LOCK, changez vers Rotate,
choisissez un cluster (ne tapez pas Align), cliquez Block, et bougez le glisseur
Y vers l’angle 109 degrées, cliquez Block, Erase, Store, refresh ( ﺡ )
l’exploreur et Load, écrivez LOCK, changez vers Rotate, un cluster (ne tapez pas
Align), cliquez Block, et bougez le glisseur Z vers 30 degrés, cliquez Block, et
maintenant cliquez Align, comme la solution S5 se trouve de nouveau dans une
position du tétraèdre qui est conforme avec le système de coordonnés trigonales.
Après écrivant UNLOCK, et cliquant Erase, Load, et Text on peut copier la
solution pivoté sur le Notepad por sauver en permanence la nouvelle solution
(par exemple dans le sélecteur de solutions dans votre copie de ma page html).
Finalement (après avoir sorti les boules marqueurs vers le bas droite) vous
pouvez cliquer Align et puis écrire MAP dans le champ de texte, et cliquer le
canvas et vous voyez la solution pivoté couche par couche.
En résumé la procédure pour pivoter une solution consiste en écrivant LOCK,
Align, Rotantion, choisir une pièce, Block, selectioner le glisseur Z, Y ou X,
et arriver à un angle voulu avec ► ou ◄ . Remarquez que le glisseurs ne sont pas
remis a zéro avec le bouton refresh ( ﺡ ) de l’exploreur, et le glisseur doit
être déplacé en dehors et de nouveau en dedans la solution qui est à recharger.
Pivoter des solutions est une manipulation complexe et il peut arriver que
recharger le browser ne suffit pas (du de fautes de procédure commis) et il faut
éteindre et rallumer l’exploreur complètement pour effacer tous les piles des
variables de plusieurs dimensions. Une dernier note concernant les glisseurs :
toujours cliquez la surface bleue du canvas 3 fois pour ne choisir aucun
cluster, avant de choisir une autre solution dans le sélecteur de solutions, ou
bien avant d’initier une opération complexe comme par exemple UNLOCK.
Pour commencer nous regardons en cas spécial WEBGL_PB_4x4x4a , construit à partir de cinq fois le même cluster en forme de P (cluster_8, _34, _35, _36, _37). Les assemblages WEBGL_PB_4x4x4b et WEBGL_PB_4x4x4c étaient importants pour l'analyse des angles car ils contiennent le tétramèr linéaire cluster_7 qui est invariant en ce qui concerne l'axe de rotation du modèle Xrot et donc permit de déterminer avec précision les combinaisons possible entre Zrot et Yrot pour le réseau cristalline le plus dense cubique. Comme exercice ouvrez les solutions et leurs diagrammes en 2D de WEBGL_PB_4x4x4b en cliquant Align, en écrivant MAP dans le champs de texte et en cliquant la toile. Dessinez sur un papier la solution en 2D tourne en sens et contre sens de la montre. Puis après avoir choisi ----- dans le scroller reconstruisez les solutions 60cw et 60ccw. En prochain exercice chargez la solution de R (solution pivoté sur la face droite du tétraèdre) et tachez de la changer en R60cw, puis en R60ccw, en appliquant des translations et rotations Zrot, Yrot et Zrot à chaque cluster, un après l'autre. N'oubliez jamais de registrer votre progrès en tapant Align et puis Store. Pour être sur je sauve mon travail régulièrement aussi en cliquant Text et Copy / Inserer sur le Notepad et sauvetage sous SOLUTION.txt dans mon système de dossiers. Comme ça je peux rechercher mon travail dans mes dossiers en cliquant le bouton Browse. Prenez note que la première boule de chaque cluster peut aussi être placé en entrant ses coordonnées (de la première boule) et angles de rotation (du cluster) en forme de X,Y,Z,Xrot,Yrot,Zrot dans le champs de texte et cliquant Align. Par exemple 0,0,3 pour placer le cluster 7 dans la solution R, R60cw et R60ccw de WEBGL_PB_4x4x4b, ou de 0,0,3,0,54.74,270 pour le cluster_7 dans la solution R de WEBGL_PB_4x4x4b.
Les deux assemblages suivantes WEBGL_PB_4x4x4d_cl1_4_8_9_12_16 et WEBGL_PB_4x4x4e_cl2_4_5_12_13_16 introduisent le cluster_12 qui est facile à placer et les cluster_16 et _13, plus difficiles à placer dans le réseau cristalline le plus dense cubique. Les clusters plats et à angles droites clusters_15 et _17 font part de l'assemblage WEBGL_PB_4x4x4l_cl15_cl17. Les autres clusters font part de WEBGL_PB_5x5x5a_cl1_3_6_7_9_10_14_15_17. Les clusters qui apparaissent en cinq paires racémiques et qui sont donc tridimensionnelles, et qui contiennent soit des angles trigonaux dans WEBGL_PB_4x4x4f_cl22_cl23 et WEBGL_PB_4x4x4g_cl24_cl25 , soit des angles trigonaux et orthogonaux WEBGL_PB_4x4x4h_cl28_cl29 , WEBGL_PB_4x4x4i_cl26_cl27 et WEBGL_PB_4x4x4k_cl30_cl31. Les clusters tridimensionnel cluster_18, _19, _20 et _21 contiennent des planes internes de miroir et ne sont donc pas racémiques et font partie de WEBGL_PB_4x4x4. Le cluster_18 est particulier par le fait que lui même forme déja une pyramide tétraédrique de PB_2x2x2, qui se place donc toujours facilement dans chaque pyramide tétraédrique. Un grand assemblage de tous les clusters décrits à aussi été fait avec quelque solutions de pyramides de 4 à 7 boules par bord: WEBGL_PBT_4to7 .
Un bon exercice pour se familiariser avec ces puzzles consiste à reconstruire des solutions publiés pour une des pyramides de 5 à 8 couches ( WEBGL_PB_5x5x5, WEBGL_PB_6x6x6, WEBGL_PB_7x7x7 and WEBGL_PB_8x8x8 ). Il y a une faute mineur dans la publication pour la pyramide de 7x7x7 par le fait que les boules avec les coordonnées 0,0,4 et 0,2,4 sont confondues, car faisant part des clusters 13 et 25 et non de 25 et 13, comme décrit.
Pas par pas procédure pour construire la pyramide 8x8x8 tétraédrique de Poly Boules
Le suivant donne une description comment construire la 8x8x8 pyramide de poly boules WEBGL_PB_8x8x8 en pas par pas: On commence par pousser les deux monomères (cluster_1 et cluster_32) de coté pour pouvoir placer la boule vert intensive du cluster_13 sur 0,0,0 , soit avec le souris ou alors en entrant 0,0,0 dans le champs de texte et ensuite cliquant Align. Oter cluster_4 et réactiver cluster_13 pour le tourner après avoir cliqué Rot (Rotate). Cliquer sur glisseur Z et tourner le cluster par + 30 dégrées en tenant la touche curseur droite > (c'est à dire dans le sens cw, ou positive au sens du système de main droite). Puis pousser le glisseur Y au maximum et le soulever le cluster_13 dans le bord gauche du tétraèdre (dans l'axe Z trigonale) en tenant la touche curseur gauche < et finir en cliquant Align. Bouger le glisseur X sur 360 dégrées et le réduire par 30 dégrées avec la touche curseur de gauche, puis Align. Cliquer Translate (Trs) et effacer tout texte dans le champs de texte et cliquer Erase et Store. On continue en plaçant cluster_4 en écrivant 1,0,0 dans le champs de texte et Align. Puis changer vers le mode bleu de Rot (ou Rotate) et tourner clustrer_4 par Zrot par environs +30 dégrées et Align, puis rechanger sur le mode de toile noir du translate et sauver par Store après avoir effacé tout texte dans le champs de texte (personnellement je sauve mes progrès toujours sous le "nom du texte vide"). Cliquez HELP pour voir le numéro des clusters dans: GLOSSARY Cluster_number <-> Cluster_names.
Bouger cluster_2 vers la gauche et remplacer par cluster_16 sur 2,0,0 et ensuite le tourner autour de Zrot par +30 dégrées par le glisseur Z et Align et effacer texte et Store. Activer cluster_23 en le cliquant deux fois et le placer sur 4,1,0 en entrant ce texte et Align. Tourner cluster_23 autour Zrot par 360-120 = +240 dégrées, Align, Translate (ou Trs), effacer texte, Store. Eloigner cluster_7 et cluster_8 transférer sur 5,2,0 en entrant ce texte puis changer vers toile bleue et Zrot par + 300 = 360 - 60 dégrées, puis Xrot par 180 dégrées, Align, Translate, effacer texte, Store (pour une meilleure lecture on ne mentionne plus tous ces cliques de routine). Notez que tous le coordonnées et angles entrés peuvent en tout moment être vérifiées en cliquant Texte après avoir sauvé le progrès. Pour le cluster_8 qu'on vient de placer on devait trouver le texte qui suit: [8,8,"4F_180_60",0.969,0,18,5.19618,0,180,0,300, .... donc Xorth=18, Yorth=5.19618,Zorth=0, Xrot=180, Yrot=0, Zrot=300, en rappelant que l'ordinateur utilise les coordonnées orthogonales et non trigonales. (Exemple Xorth = (Xtrig +1) x 3 = (5 +1) x 3 = 18, le + 1 vient du fait que les coordonnées sont contés à partir de 0. La première boule du cluster_8 se trouve dans le système orthogonale du moniteur sur X= 6 x 3 et se trouve déplacé dans la direction Y par 2 x 0.86603 x 3, le 3 étant le diamètre de chaque boule. Voir la table ci-haut pour les facteurs de conversion comme le facteur de 0.86603). Pour tout solution d'un puzzle compliqué comme pyramide poly boules 8x8x8 WEBGL_PB_8x8x8, il vaut la peine de sauver le progrès de temps à autre dans un file de texte: en cliquant Align, Store, et puis Texte et alors copier [[le texte JASON]] (JAva Script Object Notation) par Copy / Coller (ctrlC et Ctrl V) sur un ASCII éditeur de texte comme le MS Notepad et sauver ce continue sous un nom comme SOLUTION.txt dans votre système de dossiers. Pour recharger le progrès cliquer sur Browse et recharger le file SOLUTION.txt, puis bouger le curseur à travers la toile. Il est important de toujours cliquer Align avant sauver le progrès pour sauver que des valeurs contrôlées par l'algorithme du program.
Cluster_6 est placé sur 4,2,0 et doit être tourné par 300º autour Zrot et puis de 54.74° autour Xrot (ce cluster cubique se place de façon aligné en parallèle au bord du tétraèdre, donc tourné par 54.74 dégrées par rapport à la surface de base). Activer le cluster_20 et le placer sur 4,4,4 et le placer en tournant par 300° = 360°-60° autour Zrot et par 180° dégrées par Xrot. Cluster_31 monte sur 4,3,0 et doit être tourné en Zrot par 120° et on peut entrer 4,3,0,0,0,120 dans le champs de texte et cliquer Align. Cluster_22 poser sur 1,3,0 et tourner par 300° = 360° - 60° autour Zrot et Align. Cluster_24 monter sur 0,2,2 et tourner Zrot par 60° et Xrot par environs 110° (109.4°) et cliquer Align. Cluster_29 vient sur 2,3,0 et est tourné par 120° autour Zrot. La première boule de cluster_27 vient sur 0,4,0 est est tourné en position par +60° autour Zrot. Ils ne manquent que les clusters_15, _30 et _9 pour finir la couche de base avec Z=0. Lres deux premières des boules du cluster_30 restent sur la surface de base avec 2,4,0 en tournant par 60° par Zrot et par 109.4° par Xrot et on peut donc placer ce cluster en entrant 2,4,0,109.4,0,60 dans le champs de texte et Align. Notez, il est difficile de placer ce cluster et il vaut la peine de jouer avec cette pièce pour apprendre a connaitre tous les mauvaises positions possibles de cluster_30 dans la pyramide de 8x8x8. Cluster_15 est placé sur 0,2,0 et sera tourné autour Zrot par 180° et autour Yrot par 305.26° = 360° - 54.74°, comme il est placé en parallèle à une bordure du tétraèdre étant un cluster cubique. Finalement il faut encore le tourner par 30° autour Xrot (notez le voisinage "horizontale" des boules 15_4 et 13_4, donc des quatrièmes boules de cluster_15 et _13 dans la 3ième couche (Z=2) de la pyramide 8x8x8). Cluster_9 monte sur 0,7,0 et doit être tourné par 90° autour Zrot et de 234.74° = 180° + 54.74° autour Yrot pour orienter son axe Xrot dans le réseau. Finalement on tourne cluster_9 encore par 90° autour Xrot (notez que la même nomenclature de Xrot est aussi utilisé dans la programmation). Vous allez découvrir que tous ces angles peuvent être trouvés en plaçant les clusters avec soin dans la pyramide et en cliquant Align et qu'il n'est pas du tout nécessaire de les entrer dans le champs de texte! C'est l'algorithme de la fonction du Align qui fait le nécessaire pour convertir des angles approximatives en valeurs précises. Cela est primordiale comme des fautes se propagerons à travers la pyramide sans cela.
Ayant fini la couche de base, il est temps de tourner le tout en cliquant en répétition sur +45 ou -45 pour contrôler cette surface d'en dessous, car elle forme la base pour finir la deuxième couche. Cluster_2 monte sur 1,0,1 avec Zrot = 30° et Yrot = 305.26°. Le cluster_7 linéaire commence sur 0,0.,2 et étant parallèle au cluster_2, a donc les mêmes angles de rotation comme celui-ci. Cluster_19 est placé sur 6,0,1 avec Zrot = 150°, Yrot = 54.74° et Xrot = 240°. Cluster_17 commence sur 3,0,1 avec Zrot = 120° et Xrot = 125.26°. Le cluster_10, qui est aussi cubique, commence sur 2,3,1 avec Zrot = 300° et Xrot = 54.74°. Cluster_21 commence sur 0,4,2 (et ne pas sur 2,0,2) avec Zrot = 250° et Xrot = 250.53°. Cluster_25 commence sur 1,3,2 avec Zrot = 300° et Xrot = 180°. Cluster_28 passe sur 1,2,3 avec Zrot = 300° et Xrot = 174.74°. Cluster_11 est placé sur 2,0,2 avec Zrot = 150°, Yrot = 305.26° et Xrot = 240° ce qui est difficile à réussir comme ce cluster est peux visible. Dans le cas pareilles il peut aider à orienter le cluster correctement hors la pyramide, par exemple en couchant le cluster contre la surface extérieure, pour le placer finalement en entrant les positions de la première boulle dans le champs de texte, ici 2,0,2 et ensuite cliquant Align. Cluster_14 monte sur 3,0,3 avec Zrot = 150° et Xrot = 54.74°. La pyramide tétraédrique de 2x2x2 cluster_18 est posé à l'envers sur 1,1,3 avec Zrot = 270°, Yrot = 305.26° et Xrot = 54.74°. Le monomère monte sur 0,2,3 et cluster_5 sur 2,3,2 avec Zrot = 150°, Yrot = 305.26° et Xrot = 234.74°. Cluster_26 wird auf 2,2,3 et ne pas 0,3,3 avec Zrot = 330°, Yrot = 2345.74° et Xrot = 54.74°. Cluster_1' ( cluster_32 = PB_1Fa) est placé à 0,2,4 et cluster_3 à 4,0,3 avec Zrot = 150° et Yrot = 305.26°. Le cluster_12 rhombique monte sur 0,1,5 avec Zrot = 30° et le deuxième 2x2x2-tétraèdre pour finir sur 0,0,6 ce qui finit la construction de la pyramide tétraédrique de 8x8x8.
POLY BOULE OCTAÈDRES (PBO)
Introduction et définition d'assemblés d'octaèdres de poly boules, une autre manifestation possible, du le réseau cristalline le plus dense cubique
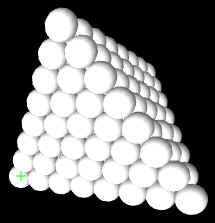
Les octaèdres de Poly Boules présentent une autre manifestation, dite habitus, du réseau cristalline le plus dense cubique, c'est à dire une autre forme macroscopique de cristallisation, autres que le tétraèdre, ou pyramide trigonale, du réseau cristalline le plus dense cubique. Puzzles de cette forme n'ont pas été définis dans la PUBLICATION pré cité, ce que nous rattrapons donc à cette occasion:
- Avec arêtes de 2 boules, l'Octaèdre en Poly Boules de 6 unités peut être construite à partir le monomère, dem dimer et le trimer l'axe de symétrie à trois temps.
- Avec arêtes de 3 boules, l'Octaèdre en Poly Boules de 19 unités peut être construite à partir de tous le clusters jusqu'au trimères, plus le tétraèdre à arêtes de deux boules.
- Avec arêtes de 4 boules, l'Octaèdre en Poly Boules de 44 unités peut être construite à partir de tous les tétramères plates de poly boules.
- Avec arêtes de 5 boules, l'Octaèdre en Poly Boules de 85 unités peut être construite à partir des mêmes clusters comme la pyramide tétraédrique de poly boules à 84 unités plus un monomère. Ce qui veut dire de tous le trimères et tétramères qui contiennent au moins une axe de symétrie à deux temps, plus tous les clusters racémiques et une seule boule.
- Avec arêtes de 6 boules, l'Octaèdre en Poly Boules de 146 unités peut être construite de tous les clusters jusqu'au tétramères (115 unités) plus les tétramères non-plates qui contiennent au moins une plaine de symétrie, donc les tridimensionnelle non-racémiques (16 unités) plus une deuxième fois de tous les clusters jusqu'au trimères (15 unités).
Bien que la structure cristalline est toujours celle du réseau cristalline le plus dense cubique, tous les angles sont à revoir, comme la position du cristal macroscopique et donc ses axes X,Y,Z ont été tourné et modifié vis-à-vis du système de coordinats orthogonaux du moniteur de l'ordinateur en comparaison avec le tétraèdre de la pyramide de poly boules trigonale.
| Angles trigonales possibles | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Angles orthogonales possibles | 90 | 180 | ||||||
| Tous les angles possibles | 30 | 60 | 90 | 120 | 150 | 180 | ||
| Angle arête-surface = | 45 | plus | 75 | 105 | 135 | 165 | 195 | 225 |
| 360 | minus | 345 | 15 | 45 | 75 | 105 | 135 | |
| Angle surface-surface = | 54.74 | plus | 84.74 | 114.74 | 144.74 | 174.74 | 204.74 | 234.74 |
| neg + | 360 | minus | 335.26 | 5.26 | 35.26 | 65.26 | 95.26 | 125.26 |
| Tous les angles possibles | 210 | 240 | 270 | 300 | 330 |
0=360 |
||
| Angle arête-surface = | 45 | plus | 255 | 285 | 315 | 345 | 15 | 45 |
| minus | 165 | 195 | 225 | 255 | 285 | 315 | ||
| Angle surface-surface = | 54.74 | plus | 264.74 | 294.74 | 324.74 | 354.74 | 24.74 | 54.74 |
| minus | 155.26 | 185.26 | 215.26 | 245.26 | 275.26 | 305.26 |
| delta-ZY | Yrot | Zrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | Xrot | |
| 001 | 315 | 45 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 324.74 | ||||||||||
| 001 | 225 | 225 | 90 | 144.74 | 215.26 | |||||||||||||||
| 00-1 | 135 | 45 | 35.26 | 144.74 | ||||||||||||||||
| 00-1 | 45 | 135 | 215.26 | |||||||||||||||||
| 00-1 | 45 | 225 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 324.74 | ||||||||||
| 010 | 0 | 90 | 0 | 45 | 54.74 | 125.26 | 180 | 234.74 | 305.26 | |||||||||||
| 010 | 180 | 270 | 0 | 180 | ||||||||||||||||
| 0-10 | 180 | 90 | 0 | |||||||||||||||||
| 0-10 | 0 | 270 | 0 | 45 | 54.74 | 125.26 | 180 | 234.74 | 305.26 | |||||||||||
| 01-1 | 45 | 135 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 330 | ||||||||||
| 01-1 | 135 | 315 | 0 | 35.26 | ||||||||||||||||
| 0-11 | 225 | 135 | 0 | 144.74 | 150 | 270 | ||||||||||||||
| 0-11 | 315 | 315 | 0 | 35.26 | 45 | 90 | 144.74 | 150 | 215.26 | 270 | 330 | |||||||||
| 100 | 0 | 0 | 0 | 45 | 54.74 | 120 | 125.26 | 180 | 234.74 | 305.26 | ||||||||||
| 100 | 180 | 180 | 125.26 | 180 | ||||||||||||||||
| -100 | 0 | 180 | 0 | 45 | 54.74 | 125.26 | 180 | 234.74 | 240 | 305.26 | ||||||||||
| -100 | 180 | 0 | 234.74 | |||||||||||||||||
| 1-10 | 0 | 300 | missing | |||||||||||||||||
| 1-10 | 180 | 120 | missing | |||||||||||||||||
| -110 | 0 | 120 | missing | |||||||||||||||||
| -110 | 180 | 300 | missing | |||||||||||||||||
| 10-1 | 45 | 315 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 324.74 | ||||||||||
| 10-1 | 135 | 135 | 0 | 35.26 | ||||||||||||||||
| 11-1 | 45 | 45 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 305.26 | 324.74 | |||||||||
| 11-1 | 135 | 225 | 0 | |||||||||||||||||
| -1-11 | 315 | 225 | 0 | 35.26 | 45 | 90 | 144.74 | 215.26 | 270 | 305.26 | 330 | |||||||||
| -1-11 | 225 | 45 | 0 | 35.26 | 144.74 | 215.26 | 330 | |||||||||||||
| -101 | 315 | 135 | 0 | 35.26 | 45 | 90 | 215.26 | 270 | 324.74 | |||||||||||
| -101 | 225 | 315 | 0 | 35.26 | 215.26 | 270 |
La plupart des octaèdres de poly boules définis sont des puzzles très difficiles à trouver une solution. Une seule solution à été trouvé, par exemple, pour l'octaèdre de quatre boules par arrête, construit selon la définition à partir des once tétramères plats. Ma recherche pour cette solution, qui durait environs 200 heures pendant 5 semaines résultait en 77 fausse solutions en remplaçant au moins un cluster de la définition par un autre, est mis en témoin pour tous les assemblages qui suivent. Les solutions d'échange sont listées dans le scroller et le clusters d'échange doivent bien sûr être présent dans l'assemblage: WEBGL_PBO_4x4x4_11x4F, WEBGL_PBO_4x4x4_11x4Fplus6x4R_26to31 , WEBGL_PBO_4x4x4_11x4Fplus1to4Fs , WEBGL_PBO_4x4x4_11x4Fplus4x4Tplus4x4R_22to25 . Tous les 77 solutions devenaient uniquement possibles par l'échange d'un cluster qui ne pouvait plus être placé dans l'espace qui restait à combler, par un autre cluster de tétramèr qui faisait l'affaire. Cette étude servait en même temps à registrer tous les angles de rotation Xrot, Yrot, Zrot pour les clusters placés dans le réseau cristalline de l'octaèdre, pivoté vis-à-vis de la pyramide de tétraèdre, comme indiqué ci-haut. Pour économiser du temps, cette étude à été achevé d'une façon moins rigoureuse que pour les pyramides à tétraèdres. Les résultats se trouvant dans la table ci-haut ont bien sûr étés utilisés pour adapter le mécanisme de Align pour l'octaèdre dans la fonction function drawBox(gl, n, viewProjMatrix, u_MvpMatrix, u_NormalMatrix) sur les lignes 2950 à 3676 dans WEBGL_PBO_4x4x4_11x4F. .
Personnellement j'ai apprécié ces travaux sur le octaèdre de poly boules comme outil exceptionnel pour encore renforcer mes capacités de visions mentaux en 3D. Pour accélérer la recherche des solutions je me suis bien sûr servi d'un modèle en bois, fait à partir de boules de bois d'un diamètre de 15mm. Ce qui se fait en moins d'une heure pour les once tétramères plats. Cela permet de rapidement essayer des variations de placement des pièces et en même temps développer une familiarité avec tous ces clusters. Pour pouvoir construire des octaèdres en poly boules il faut d'abord bricoler une pyramide égyptienne inverti, en forme une sorte "d'entonnoir de café" fait à partir de quatre triangles à arrêtes égales et posé sur un petit récipient en forme quarré. Pour pouvoir trouver des solutions il faut en premier lieu se familiariser de la façon que chacun des clusters peut être placé dans le réseau cristallin. Il faut ensuite développer une stratégie pour pouvoir réussir le puzzles. il faut par exemple reconnaitre quelles pièces sont faciles à placer dans le réseau en tous circonstances. C'est pour cela qu'il faut réserver les clusters de petite taille pour finir une solution. En conséquence les puzzles qui ne contiennent que des clusters plus grands, comme l'est le cas pour l'octaèdre de poly boules de 4x4x4, fait à partir des 11 tétramères plats, sont extrêmement difficiles à résoudre. Donc à cause de cela tous les assemblés diverses pour ce cas, contenant les candidats d'échange pour finir les fausses solutions, dont 77 sont inclus dans les scroller, ce qui documente ma recherche pour la seule bonne solution. Le premier des files, WEBGL_PBO_4x4x4_11x4F , contient dans son scroller seulement la seule et unique solution trouvée, mais cette fois encore avec les placements reçu en tournant ( _90, _180, _270 ) , pivotant ( S2, S3 ) et reflectant par une plane de mirroir (m) cette solution créant 23 placements et donc 23 "solutions" de virtualisations par l'ordinateur supplémentaires.
En ouvrant un des files ci-dessus on trouve doujours deux collections de clusters distinctes: a) les 11 pièces plats des tétramèrs qui definissent le puzzle et placé sur la surface de base Z=0; et b) un assemblages de clusters d'échange qui apparaissent plus petits en se trouvant derrière l'écran avec des Z negativs. Pour en utiliser un cluster d'échange, il faut d'abbord l'avancer vers l'observateur soit en les coordinées, où alors en cliquant x>z (ou X->Z) le tirant avec la souris, où avec le glisseur Z. Leurs placements avec des Z négatives permet de produire les diagrammes en 2D sans intérférence de ces clusters en cliquant Align, en écrivant MAP dans le champs de texte et cliquant la toile. Essayez cette procédure en ouvrant une solution pré-programmée après le chargement d'un des puzzles. Ceci en cliquant le champs du scroller à la droite du bouton Block et en choisissant une des solutions et en dèplaçant le cursor à travers la toile. Du reste, la ligne de séparaion ----- sert à ré-initialise le puzzle (en faisant cela on perd tot progrés qui n'a pas été sauvé!). Aprés avoir chargé une solution cliquez Align, écrivez MAP dans le champs de texte à la droite du bouton File et ensuite cliquez la toile. Ce qui fait apparaitre le diagram en deux dimension de la solution choisie, montrée en couche par couche vu d'en haut ( des Z positives) vers le bas (aux Z négatives), donc de la solution vue de l'observateur avec la plus grande surface de l'octaèdre placé dans la surfaçe X-Y du moniteur.
Comme toute la programmation est disponible on peut sauver la page html et l'ouvrir avec un logiciel d'éditeur ASCII (je me sers personnellement toujours de MS Frontpage) ce qui vous permet d'insérer vos propres solutions dans votre file sauvé du puzzle si vous ètes familier avec les bases du Java Script. Cherchez d'aprés la fonction function parseSolution(), pour y introduire un nouvel case ( case "maSolution": ) qui doit bien sur aussi être introduit dans la partie html du scroller dans la forme de <select id="Lock_Number" size="1" value="-1"> <option value="maSolution">maSolution_dans_le_Scroller</option>. Si donc on a trouvé une nouvelle solution au puzzle, qui on a souvé en cliquans Store et dont on à fait produire le la présentation en JASON en cliquant Texte, on peut copier / coller cette solution en forme de [[JASON-texte]] dans la fonction function parseSolution() à l'endroit de var value = ' '; entre apostrophes:
function
parseSolution()
var Solution = Lock_Number.value;
switch ( Solution ) {
case "MySolution":
var value = ' '; < insérez
le [[JASON-texte]] ici
break;
....
Comme déjà indiqué plus haut, il faut toujours assurer de placer chaque cluster avec précision dans le réseau cristalline le plus dense cubique et c'est à ce fin que nous avons programmé un algorithme pour vérifier et rectifier chaque placement en cliquant le bouton Align. Avant d'essayer de résoudre les puzzles des octaèdres il faudrait se familiariser avec les pyramides tétraédriques, qui contiennent les mêmes clusters. Pour placer des clusters je me serve souvent d'autres pièces comme aide de placement: par exemple le tétraèdre linéaire peut servir de règle. On peut bien sur aussi entrer des coordonnées et / ou des angles dans le champs de texte. Pour commencer de construire un octaèdre je place un premier cluster, par exemple dans WEBGL_PBO_4x4x4_11x4F le tétraèdre linéaire sur 0,0,-3 en écrivant ces coordonnés dans le champs de texte et cliquant Align. La boule rouge me montre donc la position du coin le plus bas de l'octaèdre, qui se trouve sur 0,0,-3 (donc avec un Z = -3). Ensuite je peux redresser cette "règle" en la tournant pour placer la quatrième boule sur la croix verte de 0,0,0. Après avoir cliqué x>z je peux placer un cluster activé avec la souris en la plaçant sur la bonne hauteur Z avec la souris en me servant de cette règle. Ensuite, après avoir cliqué z>x , je peux déplacer le cluster vers la position X-Y du moniteur désiré. Comme les couches de l'octaèdre parallèles au moniteur sont des réseaux orthogonaux, je peux me servir pour cela des clusters plats et cubiques, comme par exemple du 14 ou 15. Après chaque changement de placement toujours cliquer Align. Aussitôt que l'octaèdre prend des formes on a toujours assez de boules pour aider d'aligner correctement un nouveau cluster. Notez, même si une seule boule d'un cluster est placé sur une surface extérieur de l'octaèdre on peut le placer avec précision dans l'octaèdre en le tournant et alignant dans le bon sens à l'extérieur de l'octaèdre et le pousser après cela vers l'intérieur du corps. La dernière opération est bien sur aussi possible en entrant les coordonnés de sa première boule. Cette technique permet aussi corriger des fautes qu'on découvre en étudiant le diagramme en 2D (MAP): sélectionner le cluster, le tirer à l'extérieur, corriger son orientation et le repousser à l'intérieur de l'octaèdre.
En exercisse instructive qui permet de mieux comprendre le méchanisme du placement des clusters dans le réseau cristalline le plus dense cubique de l'octaèdre, consiste en essayant de comprendre en détail d'ou vient l'angle de rotation de 35.26° dans l'exemple qui suit. Pour placer le cluster 12 dans une des surfaces parallèle à la surface du haut vers le front de l'octaèdre il faut le tourner par Xrot = 35.26° autour le l'axe modèle du cluster. Cela aprés avoir placé le cluster en plaçant ses deux premières boulles avec un allignement dans le réseau qui se traduit dans une différence de leurs coodinées d'un delta XYZ = 0,0,1 (fait par un Zrot = 45° autour de l'axe Z et d'un Xrot = 315° autour l'axe Y du cluster). Pour comprendre l'angle de rotation Xrot il faut imaginer sa plaine de rotation qui se trouve à angle droite de l'axe Xrot. Dans cette plaine il faut ensuite construire un triangle à angle droite avec la longeur connue de deux de ses cotés de S x 1/2 x √3 et S x 1/ √2 se qui résulte dans une fraction du cosine de 0.577350(sine de 0.81655). Vue la table en dessus on calcule un angle de Xrot de 35.26° = 90° - 54.735610°.
Pour se préparer à résoudre les puzzles des octaèdres, je recommande vivement de sélectionner une dans le scroller, produire et imprimer son diagramme en 2D (cliquez Align, écrivez MAP dans le champs de texte et bouger le curseur à travers la toile). Ensuite réinstallez le puzzle en choisissant la ligne de séparation ----- dans le scroller et essayez de reconstruire la solution à partir du diagramme imprimé. Cela vous permets de vous familiariser avec les divers clusters présent. Vous allez par exemple remarquer que une fois avoir correctement placé les deux premières boules, la verte et la vert-bleue, dans le réseau cristallin en cliquant Align, il suffit de placer le cluster correctement, par une seule rotation autour Xrot (qui n'a aucun effet sur Zrot und Yrot). Prudence avec les rotations autour de Yrot en assurant que vous arrivez à une direction du cluster qui est permis dans réseau cristalline le plus dense cubique de l'octaèdre, qui résulte en incréments des coordonnées X,Y,Z permis, autrement une remise à zéro des trois angles Xrot, Yrot, Zrot à 0,0,0 dégrées peuvent résulter après deux avertissements.
Puzzles comme définis dans la PUBLICATION Crystallographic definitions for cube assemblies and ball-pyramid assemblies from poly-cubes and poly-balls, respectively |
|||
|
POLY CUBE CUBES |
POLY BALL TETRAEDRES |
POLY BALL CUBES |
POLY BALL OCTAEDRES |
|
2x2x2Cube 3x3x3Cube 3x3x3Soma 4x4x4Cube 5x5x5Cube 6x6x6Cube |
3x3x3Ball 4x4x4Ball 4x4x4cBall PBT_4to7 5x5x5Ball 6x6x6Ball 7x7x7Ball 8x8x8Ball |
WEBGL_PBC_2x2x2 WEBGL_PBC_2x2x2a WEBGL_PBC_2x2x2b WEBGL_PBC_3x3x3 WEBGL_PBC_4x4x4 WEBGL_PBC_5x5x5 WEBGL_PBC_6x6x6 |
WEBGL_PBO_2x2x2 WEBGL_PBO_3x3x3 WEBGL_PBO_4x4x4 WEBGL_PBO_4x4x4_6x4R WEBGL_PBO_4x4x4_1to4Fs WEBGL_PBO_4x4x4_4x4T-4x4R WEBGL_PBO_5x5x5 |
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
 |
 |
||
AIDE et CITATIONS
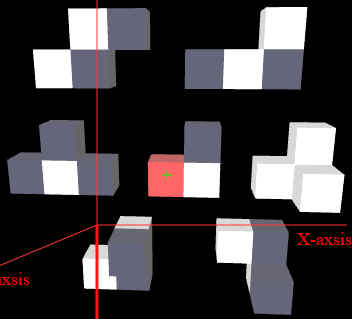
Dans tous les puzzles vous trouverez un texte d'aide en anglais en cliquant le bouton HELP, spécifique pour les puzzles des poly boules et des poly cubes Poly cubes. Des traductions en français se trouvent ici bas pour les deux versions y inclus les définitions des clusters. Des explications brefs des fonctionnalités de la surface d'utilisateurs sont données ici au lieu du fait que la plupart des commandes peuvent être découvert en jouant avec les commandes de la surface. La meilleure façon de se familiariser avec la fonctionnalités consiste à ouvrir le 2x2x2 poly cube. En dessous le toile (canvas) on trouve un nombre de boutons et glisseurs qui servent à la manipulation des clusters dans l'espace tridimensionnel. Dans la patie supérieure de la toile on retrouve les boutons et glisseurs les plus importants pour pouvoir résoudre le puzzles en réalité virtuelle (VR= Virtual Reality) en utilisant des lunettes 3D et un souris connecté pas USP avec une prise on-the-go. Le plus important de tous les boutons se trouve en haut tout à gauche et indiques Rot / Trs et permets de changer de la mode transfert au mode rotation. En mode transfert la toile est noire et an mode rotation elle est bleue.
Des mouvements en mode de transfert ou de rotations deviennent possible par la souris âpres avoir sectionné un cluster en le cliquant pour l'activer. En recliquant le cluster le mouvement est terminé, mais le cluster reste activé, comme indiqué par le texte rouge en bas sur la toile. Le texte indique Translate active cluster n (transferts du cluster n active) ou Rotate active cluster n (rotations du cluster n active) avec n indiquant l'identité du cluster active en donnant son numéro et son nom. Les trois glisseurs dénommé X, Y et Z restent actives pour le cluster activé. Un cluster reste activé aussi long que la toile ou un autre cluster ne soient pas cliqués. Notez, différent browsers peuvent montrer un comportement légèrement différents aux évènements de la surface d'utilisateur (voir ici-bas un commentaire concernant l'entrée de coordonnées orthogonaux ou de rotation dans le champs de texte).
Un problème majeur en essayant de résoudre des puzzles en 3D sur ordinateur vient du fait les les moniteurs classiques n'existent qu'en 2D. Une des trois dimensions est donc en principe toujours caché et il est d'importance de pouvoir librement tourner la vue autour le puzzle. Ce qui est achevé ici par la présence de boutons de vue de +90 +45 Tilt -45 -90, ce qui permet de tourner la vue du monde par plus ou moins 45° ou 90°. Le bouton appelé Tilt permet de pivoter la vue par 45° vue d'en haut, vue d'en pas, et vue du front. La vue en tilt est automatiquement remis en vue du front en tournant la vue du monde. Il est important de changer en permanence la vue du puzzle en plaçant les clusters pour pouvoir juger des positions spatiaux des clusters à placer dans le puzzle en construction.
Le bouton Align (pour mise en position) est une aide essentielle pour placer tous les clusters avec précision (tous deux en coordinates et en angles) dans le poly cube grandissant. Un autre bouton à deux états est la bouton dégné en X->Z ou alors en Z->X, qui permets d'inter changer le mouvement de la souris en horizontale à avoir effet sur l'axe X ou sur l'axe Z. Notez bien, que dans les positions des vues du monde diagonales de 45°, 135°, 225° et 315° ces effets sur les axes X et Z sont couplés. C'est dire qu'un du placement de la souris en horizontale a un effet sur les axes X et Z en même temps.
Les boutons de Lock (serrer) et Block (plusieurs clusters fusioné) et en plus le scroller qui contient en haut les chiffres de 1 à 5 (dont le 1 est réservé pour la solution finale) permet de sceller les clusters en un block nommé de 2 à 5 (et 1 pour sceller avec la commande LOCK). L'état de scellage est indiqué par la ligne de status en rouge en bas sur la toile. Pouvoir sceller des clusters dans des ensembles chiffrés, permet de les bouger ensemble après avoir cliqué le bouton Block (pour le moment les rotations en block ne sont pas encore possibles. En écrivant LOCK dans le champs de texte (discuté ici-bas) on peut sceller tous les clusters dans block 1, par exemple pour pouvoir bouger le premier cube à gauche en bas de la solution finale dans le centre des coordonnées (croix verte) pour ré calibrer les coordonnées de la solution. Ecrire UNLOCK dans le champs de texte permet de liberer tout les clusters de nouveau.
Les deux dernieres rangés des contrôles permettent de sauver des états intermédiates de solutions, ce qui est importante en cherchant une solution d'un des puzzles extrémement difficiles comme l'est le 5x5x5 poly cube au moindre le 6x6x6 poly cube. Deux méthodes de sauvetage ont été programmé, d'abord la plûtot volatile méthode dans le browser. Testez cette méthode avec votre browser pour le poly cube 2x2x2, car elle ne fonctionne pas avec tous les browsers qui existent. Les boutons Store, Load, Text et Erase ont été fait pour cette méthode de sauvetage et un nom peut être formulé dans le champs de texte qui apparait à droite de la désignation File (notez: on peut aussi sauver dans le browser sous le nom vide "" du file). En écrivant SOLUTION dans ce champs de texte, ou alors en cherchant une des solutions préprogrammées du scrolleur, puis bougant le cursor sur la toile, on peut aussi faire apparaitre la solution du puzzle.
En cliquant le bouton Store ou Load et après Text on peut faire apparaitre le progrés de votre solution paramétrisé en texte JASON (Java Script Object Notation) en dessous le bouton HELP, ce qui ammène à la deuxième méthode de sauver le progrès. Copiez ce texte y inclus les double paranthèses ( de [[ à ]] ) avec Ctrl C et insérez le sur MS Notepad, ou un texte éditeur similaire avec Ctrl V. Sauvez ce file de texte sur votre ordinateur (par exemple sous 2x2x2cube.txt). Vous pouvez ensuite récupérer votre solution du puzzle sauvé en cliquant le bouton Browse... et cherchant votre file (2x2x2cube.txt) pour le re-ouvrir (open). Cette deuxième méthode de sauvetage est un peux üplus compliqué comme JAVASCRIPT ne permet pas de sauver automatiquement sur un ordinateur pour raisons de sécurité. Cette deuxième méthode doit impérativement être utilisée si vous utilisez le Microsoft Internet Explorer en faisant marcher vos pages html sauvés sur le système des dossiers sauf si ils ont étés sauvés sur le serveur web Inetpup/wwwroot/... (localhost).
En écrivant VR dans le champs de texte TEXT FIELD qui se trouve à droite de mot File permets de changer vers réalité virtuelle en chargeant votre jeux en images gauche et droite pour être vue sur un téléphone mobile dans des lunettes 3D. Retapez VR dans le champs de texte pour en revenir sur la vue en mono sur une toile.
Pour des raisons instructives tout le codage de la programmation à été inclus dans chaque page de html. Aucun file de type include ou de bibliothèke ou d'API n'a été utilisé comme font le boîtes des groupes mondiaux qui courent après les profits! Du Java Script standard à été utilisé en combinaison avec le WEBGL qui à été introduit en 2015 en version du Open Graphic Language (OpenGL). Les puzzles ne marchent donc que sur les browser plus récents. Le code à été testé sur Mozzila Firefox, Chrome, normal et versions développeurs , sur Opera and on MS Explorer 11 et Microsoft Edge.
Les livres qui suivent ont été utilisées pour dévélopper le code:
E. Angel and D. Shreiner, Interactive Computer Graphics, Pearson, 7th Ed. 2015, ISBN 10: 978-1-292-01934-5.
D. Cantor and B. Jones, WEBGL Beginners Guide, 2012, PACKT, ISBN 978-1-84969-172-7.
K. Matsuda and R. Lea, WebGL Programming Guide, 2015, Adison-Wesley, ISBN 978-0-321-90292-4
Aide Poly Cubes (Traduction du Help Polycubes )
2x2x2Cube
3x3x3Cube
3x3x3Soma
4x4x4Cube
5x5x5Cube
6x6x6Cube AIDE Aide
Le but du puzzle
consiste à construire les NxNxN poly cubes avec N = 3, 4, 5, ou 6
selon quel puzzle à été sélectionné. L'arête du front d'en bas est toujours
aligné avec l'axe horizontale X du moniteur avec la surface de base placé
dans la pleine X-Y du moniteur. Le cube se développe donc en couche par
couche en direction de l'axe Z, donc vers l'observateur. Comme tous les
clusters ont étés définis en direction X, donc en état de ne pas avoir étés
tournés, il est logique que les axes Z- et Y- de rotation donnent la
définition de l'orientation du cluster dans le réseau cristallin cubic.
Il est donc essentiel de commencer par orienter chaque cluster d'abord dans
les directions de rotations Z et puis Y qui constituent la définition de
l'orientation de chaque cluster dans le réseau cristallin, et finalement
pour chaque cluster qui n'est pas linéaire, de le tourner autour l'axe X
pour pouvoir placer le 3ième et quatrième cluster, et ci de suite,
correctement dans le réseau cubic. Pour aide de placer le premier cube
d'un cluster activé (coloré en vert) avec précision sur une position
orthogonale voulu dans le réseau, le champs de texte suivant
l'indicateur File, peut être utilisé pour entrer des coordinats orthogonaux
dans la forme de 1,1,2 pour X = 1, Y = 1, Z = 2. Voir ici bas sous
Entrée de coordinats orthogonaux (Orthogonal coordinates input).
Note: soi disant serrages giratoire (gimbal locks) opeuvent avoir lieu quand
deux axes de rotations deviennent suprerposés, par exemple Xrot ou Yrot = +
ou - 90° ce qui résulte en rotations identiques ou opposées pour les deux
axes en mouvant le souris en direction verticale ou horizontale. Unew
simple remède consiste à renverser les rotations et échanger les ordres de
rotations autour des trois axes et / ou se servant des boutons x>z -
z>x. Ce problème est réduit à un minimum en se tenant sur la séquance de
rotations d'abord outour Zrot, suivi par autour Yrot et pour finir autour
Xrot. Cela parce que le premier et le deuxième cube sont placé sur l'axe de
rotation Xrot de l'espace du modèle par définition.
Movements des
Clusters (Moving Clusters)
Translate < - > Rotate
Le
control de mouvement de transfert ou de rotation par souris sont initiés en
activant un cluster choisi en le cliquant. Cliquant une deuxième fois
termine le contrôle de motion, mais le cluster reste activé, comme indiqué
par la mention rouge en bas sur la toile qui indique en anglais Translate active cluster n
(transferts du cluster n active) ou Rotate active cluster n
(rotations du cluster n active) avec n indiquant l'identité du cluster
active en donnant son numéro et son nom. Les trois glisseurs
dénommé X, Y et Z restent actives pour le cluster activé. Un cluster
reste activé aussi long que la toile ou un autre cluster ne soient pas
cliqués.
Vue (View)
les buttons +90 +45 Tilt -45 -90
permettent de tourner la vue du monde par plus ou moins 90° ou 45°.
Pivoter (Tilt)
Le bouton appelé
Tilt permet de pivoter la vue par 45° vue d'en haut, vue d'en pas, et vue
du front. La vue en tilt est automatiquement remis en vue du front en tournant
la vue du monde. Il est important de changer en permanence la vue du puzzle en
plaçant les clusters pour pouvoir juger des positions spatiaux des clusters à
placer dans le puzzle en construction.
Mise en
position (Align)
Le
bouton Align (pour mise en position) est une aide essentielle pour placer
tous les clusters avec précision (tous deux en coordinates et en angles) dans le
poly cube grandissant.
X->Z and Z->X
Un autre bouton à deux états est la bouton dégné en X->Z
ou alors en Z->X, qui permets d'inter changer le mouvement de la souris en
horizontale à avoir effet sur l'axe X ou sur l'axe Z. Notez bien, que dans
les positions des vues du monde diagonales de 45°, 135°, 225° et 315° ces effets
sur les axes X et Z sont couplés. C'est dire qu'un du placement de
la souris en horizontale a un effet sur les axes X et Z en même temps.
Serrer et Fusioner des
clusters (Lock and Block)
Les
boutons de Lock (serrer) et Block (plusieurs clusters fusioné) et en plus le
scroller qui contient en haut les chiffres de 1 à 5 (dont le 1 est réservé pour
la solution finale) permet de sceller les clusters en un block nommé de 2 à 5
(et 1 pour sceller avec la commande LOCK). L'état de scellage est indiqué par la
ligne de status en rouge en bas sur la toile. Pouvoir sceller des clusters
dans des ensembles chiffrés, permet de les bouger ensemble après avoir cliqué le
bouton Block (pour le moment les rotations en block ne sont pas encore
possibles. En écrivant LOCK dans le champs de texte (discuté ici-bas) on
peut sceller tous les clusters dans block 1, par exemple pour pouvoir bouger le
premier cube à gauche en bas de la solution finale dans le centre des
coordonnées (croix verte) pour ré calibrer les coordonnées de la solution.
Ecrire UNLOCK dans le champs de texte permet de liberer tout les clusters de
nouveau.
Sauver des solutions (Store solutions)
Les
deux dernieres rangés des contrôles permettent de sauver des états intermédiates
de solutions, ce qui est importante en cherchant une solution d'un des puzzles
extrémement difficiles comme l'est le 5x5x5 poly cube au moindre le 6x6x6 poly
cube. Deux méthodes de sauvetage ont été programmé, d'abord la plûtot volatile
méthode dans le browser. Testez cette méthode avec votre browser pour le
poly cube 2x2x2, car elle ne fonctionne pas avec tous les browsers qui existent.
Les boutons Store, Load, Text et Erase ont été fait
pour cette méthode de sauvetage et un nom peut être formulé dans le champs de
texte qui apparait à droite de la désignation File (notez: on peut aussi sauver
dans le browser sous le nom vide "" du file). En écrivant SOLUTION
dans ce champs de texte, ou alors en cherchant une des solutions préprogrammées
du scrolleur, puis bougant le cursor sur la toile, on peut aussi faire
apparaitre la solution du puzzle.
Recharger et Texte (Load and Text)
En cliquant le bouton
Store ou Load et après Text on peut faire apparaitre le
progrés de votre solution paramétrisé en texte JASON (Java
Script Object Notation) en dessous le bouton HELP, ce qui ammène à la
deuxième méthode de sauver le progrès. Copiez ce texte y inclus les double
paranthèses ( de [[ à ]]
) avec Ctrl C et insérez le sur MS Notepad, ou un texte éditeur similaire avec
Ctrl V. Sauvez ce file de texte sur votre ordinateur (par exemple sous
2x2x2cube.txt). Vous pouvez ensuite récupérer votre solution du puzzle
sauvé en cliquant le bouton Browse... et cherchant votre file
(2x2x2cube.txt) pour le re-ouvrir (open). Cette deuxième méthode de
sauvetage est un peux üplus compliqué comme JAVASCRIPT ne permet pas de sauver
automatiquement sur un ordinateur pour raisons de sécurité. Cette
deuxième méthode doit impérativement être utilisée si vous utilisez le Microsoft Internet Explorer
en faisant marcher vos pages html sauvés sur le système des dossiers sauf si ils
ont étés sauvés sur le serveur web Inetpup/wwwroot/... (localhost).
Ecrire les
mots qui suivent dans le champs de texte - ET PUIS CLIQUER LE CANVAS
(Entry into TEXT FIELD) - AND THEN CLICK THE CANVAS:
SOLUTION
pour voir la solution
VR En écrivant VR
dans le champs de texte TEXT FIELD qui se trouve à droite
de mot File permets de changer vers réalité virtuelle en chargeant votre jeux en
images gauche et droite pour être vue sur un téléphone mobile dans des lunettes
3D. Retapez VR dans le champs de texte pour en revenir sur la
vue en mono sur une toile.
PB pour changer vers les puzzles Poly Ball
dans le système cubique
(et PC pour retourner vers les Poly Cubes)
LOCK pour serrer
tous les clusters dans un seul block sous le nom block 1 (par exemple pour
la solution finale).
UNLOCK liberer tous les clusters après un
serrage.
PLAN en remplaçant ALIGN pour sauver l'arrangement présent
en forme non alligné pour la recherche de fautes dans un mapping.
MAP
pour présenter l'arrangemewnt des clusters en diageram 2D - doit être
prédédé par ALIGN (ou PLAN)
Effacer le texte dans le chams de texte (Empty Text Field)
-- > fait effacer tout le contenu de la page html sous les boutons de
commande. Il faut un un changement dans dle champs de texte!
AIDE (HELP)
-- >voir le texte de l'aide y inclus l'explication de définition des
clusters (glossary)
Coordinats orthogonaux dans la forme de 1,1,2,
ou 0,0,1, ou 1,0,3, ou 0,0,-1 ... -- > pour
placer des
clusters avec précision dans un poly cube. A) Activez le cluster choisi en le
cliquant. B) déplacez le curseur dans le champs de texte et entrez les
coodinats orthogonaux dans la forme ci dessus 0,0,2 (the coordinats
vont de 0 à 9, a leading minus
sign makes the value go negative), C) cliquez le bouton ALIGN ou cliquez la
clef ENTER de votre ordinateur, et ensuite D) bougezle curseur sur la toile.
Des angles de rotation peuventaussi être spécifiés aprés le ccordinats dans
la forme 0,0,2,180,90,270 pour
X,Y,Z,Xrot,Yrot,Zrot. Si seul les angles doivent être
changés entrez ,,,180,90,270 ( notez les paramètres à ne pas changer
sont présentez par des vides - devant ou entre entre commas). Si vous
utilisez MS internet Explorer seul cliquer le bouton ALIGN peut faire entrer
les valeurs séparés par des virgules venant d'unchamps de texte (comma
separated values in a web form).
Pour
des raisons instructives tout le codage de la programmation à été inclus dans
chaque page de html. Aucun file de type include ou de bibliothèke ou d'API
n'a été utilisé comme font le boîtes des groupes mondiaux qui courent après les
profits! Du Java Script standard à été utilisé en combinaison avec le WEBGL qui
à été introduit en 2015 en version du Open Graphic Language (OpenGL). Les
puzzles ne marchent donc que sur les browser plus récents. Le code à été
testé sur Mozzila Firefox, Chrome, normal et versions développeurs ,
sur Opera and on MS Explorer 11 et Microsoft Edge.
The following books have been used to develop the code:
E. Angel and D. Shreiner, Interactive Computer Graphics, Pearson, 7th Ed. 2015, ISBN 10: 978-1-292-01934-5.
D. Cantor and B. Jones, WEBGL Beginners Guide, 2012, PACKT, ISBN 978-1-84969-172-7.
K. Matsuda and R. Lea, WebGL Programming Guide, 2015, Adison-Wesley, ISBN 978-0-321-90292-4
GLOSSARY Cluster_number <-> Cluster_names
1=cluster 2=clustname
1 PC_1F
2 PC_2F
3 PC_3F_180
4 PC_3F_90
5 PC_4F_180_180
6 PC_4F_180_90
7 PC_4F_90_270
8 PC_4F_90_90
9 PC_4F_180y90
10 PC_4T_90y0
11 PC_4R_90_0
12 PC_4R_270_0
13 PC_5F_180_180_180
14 PC_5F_180_180_90
15 PC_5F_180_90_180
16 PC_5F_180_90_270
17 PC_5F_90_180_90
18 PC_5F_90_180_270
19 PC_5F_90_270_90
20 PC_5F_180_90_90
21 PC_5F_180_180y90
22 PC_5F_90y180y270
23 PC_5F_180_90y270
24 PC_5F_90y180y270
25 PC_5T_90_90_0
26 PC_5T_90_0_90 equals:
27 PC_5T_180_90y0
28 PC_5T_180y90_0
29 PC_5T_180y90y0
30 PC_5R_180_90_0
31 PC_5R_180_270_0
32 PC_5R_90_270_0
33 PC_5R_270_90_0
34 PC_5R_90_180y0
35 PC_5R_270_180y0
36 PC_5R_90_270y0
37 PC_5R_270_90y0
38 PC_5R_90_180_0
39 PC_5R_270_180_0
40 PC_5R_90_0_270
41 = 1bis PC_1Fbis
3x3x3Ball 4x4x4Ball 4x4x4PBT_4to7 5x5x5Ball 6x6x6Ball 7x7x7Ball 8x8x8Ball
AIDE
Le but du puzzle
consiste à construire les NxNxN poly boule tétraèdre avec N = 3, 4, 5,
6, 7 ou 8
selon quel puzzle à été sélectionné. L'arête du front d'en bas est toujours
aligné avec l'axe horizontale X du moniteur avec la surface de base placé
dans la pleine X-Y du moniteur. La pyramide se développe donc en couche par
couche en direction de l'axe Z, donc vers l'observateur. Comme tous les
clusters ont étés définis en direction X, donc en état de ne pas avoir étés
tournés, il est logique que les axes Z- et Y- de rotation donnent la
définition de l'orientation du cluster dans le réseau cristallin de boules
le plus dense cubic.
Il est donc essentiel de commencer par orienter chaque cluster d'abord dans
les directions de rotations Z et puis Y qui constituent la définition de
l'orientation de chaque cluster dans le réseau cristallin, et finalement
pour chaque cluster qui n'est pas linéaire, de le tourner autour l'axe X
pour pouvoir placer le 3ième et quatrième boule, et ci de suite,
correctement dans le réseau cristallin. Pour aide de placer la première
boule
d'un cluster activé (coloré en vert) avec précision sur une position
trigonale voulu dans le réseau, le champs de texte suivant
l'indicateur File, peut être utilisé pour entrer des coordinats trigonaux
dans la forme de 1,1,2 pour Xtrig = 1, Ytrig = 1, Ztrig = 2. Voir ici bas sous
Entrée de coordinats trigoneaux (trigonal coordinates input).
Note: soi disant serrages giratoire (gimbal locks) opeuvent avoir lieu quand
deux axes de rotations deviennent suprerposés, par exemple Xrot ou Yrot = +
ou - 90° ce qui résulte en rotations identiques ou opposées pour les deux
axes en mouvant le souris en direction verticale ou horizontale. Unew
simple remède consiste à renverser les rotations et échanger les ordres de
rotations autour des trois axes et / ou se servant des boutons x>z -
z>x. Ce problème est réduit à un minimum en se tenant sur la séquance de
rotations d'abord outour Zrot, suivi par autour Yrot et pour finir autour
Xrot. Cela parce que le premier et le deuxième cube sont placé sur l'axe de
rotation Xrot de l'espace du modèle par définition.
Movements des
Clusters (Moving Clusters)
Translate < - > Rotate
Le
control de mouvement de transfert ou de rotation par souris sont initiés en
activant un cluster choisi en le cliquant. Cliquant une deuxième fois
termine le contrôle de motion, mais le cluster reste activé, comme indiqué
par la mention rouge en bas sur la toile qui indique en anglais Translate active cluster n
(transferts du cluster n active) ou Rotate active cluster n
(rotations du cluster n active) avec n indiquant l'identité du cluster
active en donnant son numéro et son nom. Les trois glisseurs
dénommé X, Y et Z restent actives pour le cluster activé. Un cluster
reste activé aussi long que la toile ou un autre cluster ne soient pas
cliqués.
Vue (View)
les buttons +90 +45 Tilt -45 -90
permettent de tourner la vue du monde par plus ou moins 90° ou 45°.
Pivoter (Tilt)
Le bouton appelé
Tilt permet de pivoter la vue par 45° vue d'en haut, vue d'en pas, et vue
du front. La vue en tilt est automatiquement remis en vue du front en tournant
la vue du monde. Il est important de changer en permanence la vue du puzzle en
plaçant les clusters pour pouvoir juger des positions spatiaux des clusters à
placer dans le puzzle en construction.
Mise en
position (Align)
Le
bouton Align (pour mise en position) est une aide essentielle pour placer
tous les clusters avec précision (tous deux en coordinates et en angles) dans le
poly cube grandissant.
X->Z and Z->X
Un autre bouton à deux états est la bouton dégné en X->Z
ou alors en Z->X, qui permets d'inter changer le mouvement de la souris en
horizontale à avoir effet sur l'axe X ou sur l'axe Z. Notez bien, que dans
les positions des vues du monde diagonales de 45°, 135°, 225° et 315° ces effets
sur les axes X et Z sont couplés. C'est dire qu'un du placement de
la souris en horizontale a un effet sur les axes X et Z en même temps.
Serrer et Fusioner des
clusters (Lock and Block)
Les
boutons de Lock (serrer) et Block (plusieurs clusters fusioné) et en plus le
scroller qui contient en haut les chiffres de 1 à 5 (dont le 1 est réservé pour
la solution finale) permet de sceller les clusters en un block nommé de 2 à 5
(et 1 pour sceller avec la commande LOCK). L'état de scellage est indiqué par la
ligne de status en rouge en bas sur la toile. Pouvoir sceller des clusters
dans des ensembles chiffrés, permet de les bouger ensemble après avoir cliqué le
bouton Block (pour le moment les rotations en block ne sont pas encore
possibles. En écrivant LOCK dans le champs de texte (discuté ici-bas) on
peut sceller tous les clusters dans block 1, par exemple pour pouvoir bouger le
premier cube à gauche en bas de la solution finale dans le centre des
coordonnées (croix verte) pour ré calibrer les coordonnées de la solution.
Ecrire UNLOCK dans le champs de texte permet de liberer tout les clusters de
nouveau.
Sauver des solutions (Store solutions)
Les
deux dernieres rangés des contrôles permettent de sauver des états intermédiates
de solutions, ce qui est importante en cherchant une solution d'un des puzzles
extrémement difficiles comme l'est le 5x5x5 poly cube au moindre le 6x6x6 poly
cube. Deux méthodes de sauvetage ont été programmé, d'abord la plûtot volatile
méthode dans le browser. Testez cette méthode avec votre browser pour le
poly cube 2x2x2, car elle ne fonctionne pas avec tous les browsers qui existent.
Les boutons Store, Load, Text et Erase ont été fait
pour cette méthode de sauvetage et un nom peut être formulé dans le champs de
texte qui apparait à droite de la désignation File (notez: on peut aussi sauver
dans le browser sous le nom vide "" du file). En écrivant SOLUTION
dans ce champs de texte, ou alors en cherchant une des solutions préprogrammées
du scrolleur, puis bougant le cursor sur la toile, on peut aussi faire
apparaitre la solution du puzzle.
Recharger et Texte (Load and Text)
En cliquant le bouton
Store ou Load et après Text on peut faire apparaitre le
progrés de votre solution paramétrisé en texte JASON (Java
Script Object Notation) en dessous le bouton HELP, ce qui ammène à la
deuxième méthode de sauver le progrès. Copiez ce texte y inclus les double
paranthèses ( de [[ à ]]
) avec Ctrl C et insérez le sur MS Notepad, ou un texte éditeur similaire avec
Ctrl V. Sauvez ce file de texte sur votre ordinateur (par exemple sous
2x2x2cube.txt). Vous pouvez ensuite récupérer votre solution du puzzle
sauvé en cliquant le bouton Browse... et cherchant votre file
(2x2x2cube.txt) pour le re-ouvrir (open). Cette deuxième méthode de
sauvetage est un peux üplus compliqué comme JAVASCRIPT ne permet pas de sauver
automatiquement sur un ordinateur pour raisons de sécurité. Cette
deuxième méthode doit impérativement être utilisée si vous utilisez le Microsoft Internet Explorer
en faisant marcher vos pages html sauvés sur le système des dossiers sauf si ils
ont étés sauvés sur le serveur web Inetpup/wwwroot/... (localhost).
Ecrire les
mots qui suivent dans le champs de texte - ET PUIS CLIQUER LE CANVAS
(Entry into TEXT FIELD) - AND THEN CLICK THE CANVAS:
SOLUTION
pour voir la solution
VR En écrivant VR
dans le champs de texte TEXT FIELD qui se trouve à droite
de mot File permets de changer vers réalité virtuelle en chargeant votre jeux en
images gauche et droite pour être vue sur un téléphone mobile dans des lunettes
3D. Retapez VR dans le champs de texte pour en revenir sur la
vue en mono sur une toile.
LOCK pour serrer
tous les clusters dans un seul block sous le nom block 1 (par exemple pour
la solution finale).
UNLOCK liberer tous les clusters après un
serrage.
PLAN en remplaçant ALIGN pour sauver l'arrangement présent
en forme non alligné pour la recherche de fautes dans un mapping.
MAP
pour présenter l'arrangemewnt des clusters en diageram 2D - doit être
prédédé par ALIGN (ou PLAN)
Effacer le texte dans le chams de texte (Empty Text Field)
-- > fait effacer tout le contenu de la page html sous les boutons de
commande. Il faut un un changement dans dle champs de texte!
AIDE (HELP)
-- >voir le texte de l'aide y inclus l'explication de définition des
clusters (glossary)
Coordinats trigonaux dans la forme de 1,1,2,
ou 0,0,1, ou 1,0,3, ou 0,0,-1 ... -- > pour
placer des
clusters avec précision dans une pyramide poly boule. A) Activez le cluster
choisi en le cliquant. B) déplacez le curseur dans le champs de texte et
entrez les coodinats orthogonaux dans la forme ci dessus 0,0,2 (the coordinats
vont de 0 à 9, a leading minus
sign makes the value go negative), C) cliquez le bouton ALIGN ou cliquez la
clef ENTER de votre ordinateur, et ensuite D) bougez le curseur sur la
toile. Des angles de rotation peuvent aussi être spécifiés aprés le
ccordinats dans la forme 0,0,2,180,90,270 pour
Xtrig,Ytrig,Ztrig,Xrot,Yrot,Zrot. Si seul les angles
doivent être changés entrez ,,,180,90,270 (notez les paramètres à ne
pas changer sont présentez par des vides - devant ou entre entre commas).
Si vous utilisez MS internet Explorer seul cliquer le bouton ALIGN peut
faire entrer les valeurs séparés par des virgules venant d'unchamps de texte
(comma separated values in a web form).
Pour
des raisons instructives tout le codage de la programmation à été inclus dans
chaque page de html. Aucun file de type include ou de bibliothèke ou d'API
n'a été utilisé comme font le boîtes des groupes mondiaux qui courent après les
profits! Du Java Script standard à été utilisé en combinaison avec le WEBGL qui
à été introduit en 2015 en version du Open Graphic Language (OpenGL). Les
puzzles ne marchent donc que sur les browser plus récents. Le code à été
testé sur Mozzila Firefox, Chrome, normal et versions développeurs ,
sur Opera and on MS Explorer 11 et Microsoft Edge.
The following books have been used to develop the code:
E. Angel and D. Shreiner, Interactive Computer Graphics, Pearson, 7th Ed. 2015, ISBN 10: 978-1-292-01934-5.
D. Cantor and B. Jones, WEBGL Beginners Guide, 2012, PACKT, ISBN 978-1-84969-172-7.
K. Matsuda and R. Lea, WebGL Programming Guide, 2015, Adison-Wesley, ISBN 978-0-321-90292-4
GLOSSARY Cluster_number <-> Cluster_names
1=cluster 2=clustname
1 PB_1F
2 PB_2F
3 PB_3F_180
4 PB_3F_60
5 PB_3F_120
6 PB_3F_90
7 PB_4F_180_180
8 PB_4F_180_60
9 PB_4F_180_120
10 PB_4F_180_90
11 PB_4F_120_120
12 PB_4F_60y120
13 PB_4F_120_240
14 PB_4F_90_90
15 PB_4F_90_270
16 PB_4F_120y240
17 PB_4F_90y180
18 PB_4T_60y60
19 PB_4T_60y120
20 PB_4T_60_90
21 PB_4T_90y120
22 PB_4R_120_120
23 PB_4R_240_240
24 PB_4R_120_240
25 PB_4R_240_120
26 PB_4R_90_120
27 PB_4R_270_240
28 PB_4R_90_240
29 PB_4R_270_120
30 PB_4R_60y90
31 PB_4R_300y270
32 PB_1Fa
33 PB_4T_60_60a
34 PB_4F_180_60b
35 PB_4F_180_60c
36 PB_4F_180_60c
37 PB_4F_180_60d